Question

【题目】如图，在直三棱柱中，是上的一点，，且.

（1）求证：平面；

（2）若，求点到平面的距离.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）连接A1B交AB1于E，连接DE，根据中位线定理即可得出DE∥A1C，故而A1C∥平面AB1D1；

（2）过B作BF⊥B1D，则可证BF⊥平面AB1D，于是点A1到平面AB1D的距离等于C到平面AB1D的距离，等于B到平面AB1D的距离BF．

（1）如图，

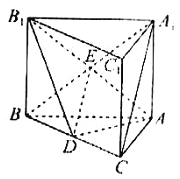
连接，交于点，再连接，

据直棱柱性质知，四边形为平行四边形，为的中点，

∵当时，，∴是的中点，∴，

又平面，平面，∴平面.

（2）如图，在平面中，过点作，垂足为，

∵是中点，

∴点到平面与点到平面距离相等，

∵平面，∴点到平面的距离等于点到平面的距离，

∴长为所求，在中，，，，

∴，∴点到平面的距离为.