练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．在如图所示的矩形ABCD中，AB=2，AD=1，E为线段BC上的点，则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为（　　）
    A．2B．4C．$\frac{17}{4}$D．$\frac{15}{4}$

    分析 以BC所在直线为x轴，BA所在直线为y轴建立平面直角坐标系，可得A（0，2），D（1，2），设E（x，0）（0≤x≤1），得到$\overrightarrow{AE}、\overrightarrow{DE}$的坐标，代入$\overrightarrow{AD}•\overrightarrow{DE}$，展开后利用配方法求得$\overrightarrow{AD}•\overrightarrow{DE}$的最小值．

    解答 解：以BC所在直线为x轴，BA所在直线为y轴建立平面直角坐标系，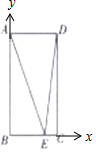
    则A（0，2），D（1，2），设E（x，0）（0≤x≤1），
    则$\overrightarrow{AE}=（x，-2）$，$\overrightarrow{DE}=（x-1，-2）$．
    ∴$\overrightarrow{AE}•\overrightarrow{DE}$=（x，-2）•（x-1，-2）=x2-x+4=$（x-\frac{1}{2}）^{2}+\frac{15}{4}$．
    ∵0≤x≤1，
    ∴$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为：$\frac{15}{4}$．
    故选：D．

    点评 本题考查平面向量的数量积运算，利用建系起到事半功倍的效果，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点分别为F1，F2，点$P（{-1，\frac{{2\sqrt{3}}}{3}}）$在椭圆C上，|PF2|=$\frac{{4\sqrt{3}}}{3}$，过点F1的直线l与椭圆C分别交于M，N两点．
    （1）求椭圆C的标准方程和离心率；
    （2）若△OMN的面积为$\frac{12}{11}$，O为坐标原点，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．设M是椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$上的一点，F1，F2为焦点，且$∠{F_1}M{F_2}=\frac{π}{3}$，则△MF1F2的面积为（　　）
    A．3B．$16（2+\sqrt{3}）$C．$16（2-\sqrt{3}）$D．$3\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．参数方程$\left\{\begin{array}{l}x=4cosθ\\ y=3sinθ\end{array}$（θ为参数）表示的曲线是（　　）
    A．以$（{±\sqrt{7}，0}）$为焦点的椭圆B．以（±4，0）为焦点的椭圆
    C．离心率为$\frac{{\sqrt{7}}}{5}$的椭圆D．离心率为$\frac{3}{5}$的椭圆

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知|$\overrightarrow{a}$|=1，$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$，（$\overrightarrow{a}$-$\overrightarrow{b}$）•（$\overrightarrow{a}$+$\overrightarrow{b}$）=$\frac{1}{2}$．
    （1）求向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ；
    （2）求|$\overrightarrow{a}$+$\overrightarrow{b}$|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．如果$\frac{x^2}{4}+\frac{y^2}{m}=1$表示焦点在x轴的椭圆，则实数m的取值范围是（　　）
    A．（0，4]B．（0，4）C．（4，+∞）D．[4，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．设数列{an}满足：a1=a，an+1=$\frac{2{a}_{n}}{{a}_{n}^{2}+1}$（a＞0且a≠1，n∈N*）．
    （1）证明：当n≥2时，an＜an+1＜1；
    （2）若b∈（a2，1），求证：当整数k≥$\frac{（b-{a}_{2}）（b+1）}{{a}_{2}（1-b）}$+1时，ak+1＞b．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

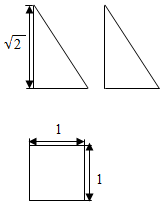    20．某几何体的三视图如图所示，设该几何体中最长棱所在的直线为m，与直线m不相交的其中一条棱所在直线为n，则直线m与n所成的角为$\frac{π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=x3-x2-3，g（x）=$\frac{a}{x}$+xlnx的定义域都是[$\frac{1}{2}$，2]
    （1）求f（x）的最大值；
    （2）若对任意的s，t∈[$\frac{1}{2}$，2]都有f（s）≤g（t）成立，求a的范围．

    查看答案和解析>>

    同步练习册答案