
某商场预计从2013年1月份起的前x个月,顾客对某商品的需求总量p(x)(单位:件)与x的关系近似的满足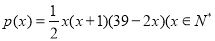 ,且
,且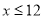 )。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
)。该商品第x月的进货单价q(x)(单位:元)与x的近似关系是
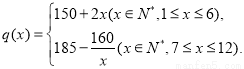
(1)写出这种商品2013年第x月的需求量f(x)(单位:件)与x的函数关系式;
(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问该商场2013年第几个月销售该商品的月利润最大,最大月利润为多少元?
(1)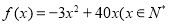 ,且
,且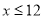 );(2)3125;
);(2)3125;
【解析】
试题分析:(1)当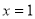 时,需求量为
时,需求量为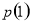 ,当
,当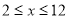 时,2013年第
时,2013年第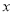 个月的总需求量等于第
个月的总需求量等于第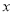 个月的需求总量减去第
个月的需求总量减去第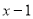 个月需求总量;(2)根据利润=该商品每件的利润
个月需求总量;(2)根据利润=该商品每件的利润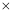 月销售量,来列出利润的函数关系式,然后通过求导数讨论函数单调性来求函数的最值即可;
月销售量,来列出利润的函数关系式,然后通过求导数讨论函数单调性来求函数的最值即可;
试题解析:【解析】
(1)当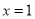 时,
时, , 2分
, 2分
当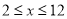 ,且
,且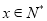 时,
时,
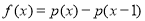
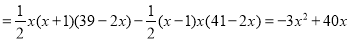 。 4分
。 4分
经验证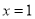 符合
符合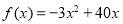 。
。
故2013年第x月的需求量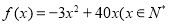 ,且
,且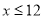 )。 5分
)。 5分
(2)该商场预计第x月销售该商品的月利润为
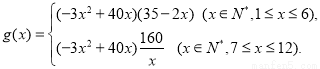 7分
7分
即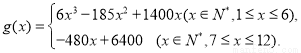 8分
8分
当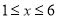 时,
时,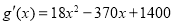 ,
,
令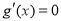 ,解得
,解得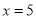 或
或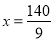 (舍去)。
(舍去)。
所以,当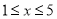 时,
时, ;当
;当 时,
时,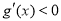 。
。
当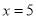 时,
时,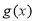 的最大值为
的最大值为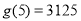 元。 10分
元。 10分
当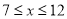 时,
时,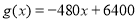 是减函数,
是减函数,
所以,当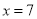 时,
时,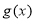 的最大值为
的最大值为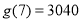 元。 12分
元。 12分
综上,该商场2013年第5个月销售该商品的月利润最大,最大月利润为3125元。13分
考点:利用导数求最值问题;


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源:2014-2015学年河南省富洲部高二上学期9月考试数学试卷(解析版) 题型:解答题
在△ABC中,角A,B,C的对边分别是a,b,c , ,
,
(1)若 ,求
,求 的值.
的值.
(2)若△ABC是锐角三角形时,求 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知从A口袋中摸出一个球是红球的概率为 ,从B口袋中摸出一个球是红球的概率为
,从B口袋中摸出一个球是红球的概率为 。现从两个口袋中各摸出一个球,那么这两个球中没有红球的概率是( )
。现从两个口袋中各摸出一个球,那么这两个球中没有红球的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省高二10月月考数学试卷(解析版) 题型:解答题
己知等比数列 所有项均为正数,首项
所有项均为正数,首项 ,且
,且 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)数列 的前n项和为
的前n项和为 ,若S6=63,求实数
,若S6=63,求实数 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com