练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数，则＝____________。

     

    0

    【解析】

    试题分析：，所以

    考点：导数公式的应用

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届北京市高三8月开学测试数学试卷（解析版） 题型：填空题

    已知，，是虚数单位.若与互为共轭复数，则 .

     

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年河南省洛阳市高一10月月考数学试卷（解析版） 题型：填空题

    若是一次函数，且，则= _________________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年河南省西区高一9月月考数学试卷（解析版） 题型：解答题

    （本小题12分）

    已知函数，,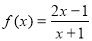

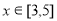    ⑴ 判断函数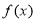的单调性，并证明；

    ⑵ 求函数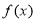的最大值和最小值．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届北京市西城区高二下学期期末考试理科数学试卷（解析版） 题型：填空题

    已知函数，且是函数的极值点。给出以下几个问题：

    ①；②；③；④

    其中正确的命题是__________。（填出所有正确命题的序号）

     

    查看答案和解析>>

    科目：高中数学 来源：2015届北京市西城区高二下学期期末考试理科数学试卷（解析版） 题型：选择题

    如果用反证法证明“数列的各项均小于2”，那么应假设（ ）

    A.数列的各项均大于2

    B.数列的各项均大于或等于2

    C.数列中存在一项

    D.数列中存在一项，

     

    查看答案和解析>>

    科目：高中数学 来源：2015届北京市西城区高二下学期期末考试文科数学试卷（解析版） 题型：解答题

    某商场预计从2013年1月份起的前x个月，顾客对某商品的需求总量p（x）（单位：件）与x的关系近似的满足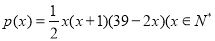，且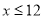）。该商品第x月的进货单价q（x）（单位：元）与x的近似关系是

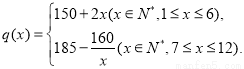
    （1）写出这种商品2013年第x月的需求量f（x）（单位：件）与x的函数关系式；

    （2）该商品每件的售价为185元，若不计其他费用且每月都能满足市场需求，试问该商场2013年第几个月销售该商品的月利润最大，最大月利润为多少元？

     

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年河南省西区高一9月月考数学试卷（解析版） 题型：选择题

    下列四个函数中，在上是增函数的是（ ）

    A . B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年河南省高二上学期期中考试文科数学试卷（解析版） 题型：选择题

    在中，角所对应的边分别为，.若,则（ ）

    A. B.3 C.或3 D.3或

     

    查看答案和解析>>

    同步练习册答案