
如图,函数f(x)=x+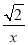 的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.

(1)证明:|PM|·|PN|为定值;
(2)O为坐标原点,求四边形OMPN面积的最小值.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-7抛物线(解析版) 题型:填空题
设斜率为1的直线l过抛物线y2=ax(a>0)的焦点F,且和y轴交于点A,若△OAF(O为坐标原点)的面积为8,则a的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-4直线与圆、圆与圆的位置关系(解析版) 题型:选择题
直线ax+by+c=0与圆x2+y2=9相交于两点M、N,若c2=a2+b2,则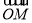 ·
·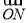 (O为坐标原点)等于( )
(O为坐标原点)等于( )
A.-7 B.-14 C.7 D.14
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-3圆的方程(解析版) 题型:解答题
已知圆C经过P(4,-2),Q(-1,3)两点,且在y轴上截得的线段长为4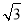 ,半径小于5.
,半径小于5.
(1)求直线PQ与圆C的方程;
(2)若直线l∥PQ,且l与圆C交于点A,B,且以线段AB为直径的圆经过坐标原点,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-3圆的方程(解析版) 题型:选择题
过点M(1,2)的直线l将圆(x-2)2+y2=9分成两段弧,当其中的劣弧最短时,直线的方程是( )
A.x=1 B.y=1
C.x-y+1=0 D.x-2y+3=0
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-2直线的交点坐标与距离公式(解析版) 题型:解答题
已知直线l经过直线2x+y-5=0与x-2y=0的交点.
(1)点A(5,0)到l的距离为3,求l的方程;
(2)求点A(5,0)到l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-2直线的交点坐标与距离公式(解析版) 题型:选择题
已知点P在y=x2上,且点P到直线y=x的距离为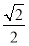 ,这样的点P的个数是( )
,这样的点P的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-1直线的倾斜角与斜率、直线方程(解析版) 题型:选择题
已知直线l:ax+y-2-a=0在x轴和y轴上的截距相等,则a的值是( )
A.1 B.-1 C.-2或-1 D.-2或1
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:选择题
如图(a),在正方形ABCD中,E、F分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为H,如图(b)所示,那么,在四面体A-EFH中必有( )
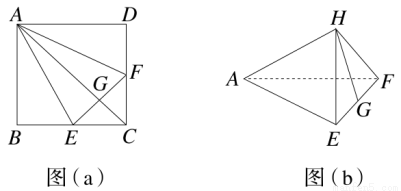
A.AH⊥△EFH所在平面
B.AG⊥△EFH所在平面
C.HF⊥△AEF所在平面
D.HG⊥△AEF所在平面
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com