
 的正方形ABCD沿对角线AC折成直二面角,使D到P的位置.
的正方形ABCD沿对角线AC折成直二面角,使D到P的位置.
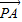 与
与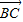 的夹角求解,注意与直线所成角的关系;
的夹角求解,注意与直线所成角的关系; =(-λ,λ,0)),
=(-λ,λ,0)),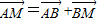 =(1,1,0)+(-λ,λ,0)=(1-λ,1+λ,0),可求平面PAM的一个法向量,易知平面PAC的一个法向量为
=(1,1,0)+(-λ,λ,0)=(1-λ,1+λ,0),可求平面PAM的一个法向量,易知平面PAC的一个法向量为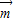 =(1,0,0),
=(1,0,0),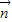 ,
,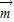 >|=
>|= ,利用向量夹角公式可得关于λ的方程,解出即可;
,利用向量夹角公式可得关于λ的方程,解出即可;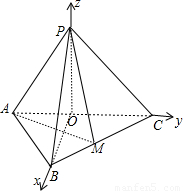 解:(1)取AC中点O,连接PO、OB,以O为原点建立如图所示的空间直角坐标系,
解:(1)取AC中点O,连接PO、OB,以O为原点建立如图所示的空间直角坐标系,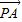 =(0,-1,-1),
=(0,-1,-1),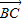 =(-1,1,0),
=(-1,1,0),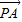 ,
,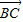 >=
>=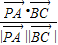 =
=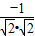 =-
=- ,
,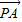 ,
,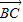 >=120°,直线PA与BC所成的角为60°;
>=120°,直线PA与BC所成的角为60°;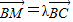 =(-λ,λ,0),
=(-λ,λ,0),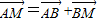 =(1,1,0)+(-λ,λ,0)=(1-λ,1+λ,0),
=(1,1,0)+(-λ,λ,0)=(1-λ,1+λ,0),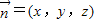 为平面PAM的一个法向量,则
为平面PAM的一个法向量,则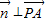 ,
,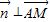 ,
,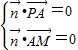 ,即
,即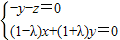 ,取
,取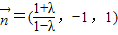 ,
,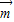 =(1,0,0),
=(1,0,0),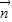 ,
,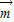 >|=
>|=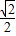 ,即
,即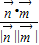 =
=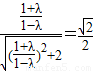 ,
,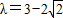 ,
,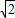 时,平面PAC与平面PAM所成的锐二面角为45°.
时,平面PAC与平面PAM所成的锐二面角为45°.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
 已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,
已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,| FM |
| 1 |
| 2 |
| FA |
A、3
| ||
B、
| ||
C、2
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
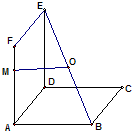 已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,
已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,| FM |
| 1 |
| 3 |
| FA |
A、3
| ||
B、
| ||
C、2
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
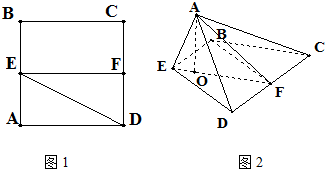 已知边长为2的正方形ABCD,E,F分别是AB,CD的中点,将△ADE沿DE折起,点A在平面BCDE的投影点O恰好落在直线EF上.
已知边长为2的正方形ABCD,E,F分别是AB,CD的中点,将△ADE沿DE折起,点A在平面BCDE的投影点O恰好落在直线EF上.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com