
分析 (1)令x取x+1代入$f(x+1)=\frac{1-f(x)}{1+f(x)}$化简后,由函数周期性的定义即可证明结论;
(2)由x∈[-1,0)得x+1∈[0,1),求出f(x+1)代入$f(x+1)=\frac{1-f(x)}{1+f(x)}$化简后求出f(x),即可求出一个周期[-1,1)上的解析式,利用函数的周期性求出f(x)在x∈[2k-1,2k+1)(k∈Z)时的解析式;
(3)由(2)和函数的周期性画出f(x)的图象,将方程根的问题转化为图象的交点问题,根据图象和条件对a分类讨论,分别结合图象和条件列出不等式组求出a的取值范围.
解答 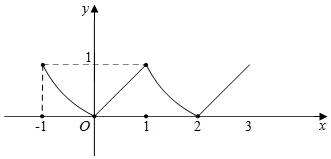 证明:(1)因为$f(x+1)=\frac{1-f(x)}{1+f(x)}$,令x取x+1得,
证明:(1)因为$f(x+1)=\frac{1-f(x)}{1+f(x)}$,令x取x+1得,
所以$f(x+2)=\frac{1-f(x+1)}{1+f(x+1)}=\frac{{1-\frac{1-f(x)}{1+f(x)}}}{{1+\frac{1-f(x)}{1+f(x)}}}=f(x)$,
所以,2是函数f(x)的周期.
解:(2)当x∈[-1,0)时,x+1∈[0,1),则f(x+1)=x+1,
又$f(x+1)=\frac{1-f(x)}{1+f(x)}$,即$\frac{1-f(x)}{1+f(x)}=x+1$,解得$f(x)=-\frac{x}{x+2}$.
所以,当x∈[-1,0)时,$f(x)=-\frac{x}{x+2}$.
所以,$f(x)=\left\{\begin{array}{l}-\frac{x}{x+2}\;,\;x∈[-1\;,\;0)\;\\ x\;\;\;,\;x∈[0\;,\;1)\;.\end{array}\right.$
因为f(x)的周期为2,所以当x∈[2k-1,2k+1)(k∈Z)时,
f(x)=f(x-2k)=$\left\{\begin{array}{l}{-\frac{x-2k}{x-2k+2},x∈[2k-1,2k)}\\{x-2k,[2k,2k+1)}\end{array}\right.$,
(3)由(2)作出函数的图象,则方程f(x)=ax解的个数:
就是函数f(x)的图象与直线y=ax的交点个数.
若a=0,则x=2k(k∈Z)都是方程的解,
不合题意.
若a>0,则x=0是方程的解.
要使方程恰好有20个解,在区间[1,19)上,f(x)有9个周期,每个周期有2个解,
在区间[19,21)上有且仅有一个解.
则$\left\{\begin{array}{l}19a<1\;\\ 21a>1\;\end{array}\right.$解得,$\frac{1}{21}<a<\frac{1}{19}$.
若a<0,同理可得$-\frac{1}{19}<a<-\frac{1}{21}$.
综上,$a∈({-\frac{1}{19}\;,\;-\frac{1}{21}})∪({\frac{1}{21}\;,\;\frac{1}{19}})$.
点评 本题考查了函数周期性以及解析式,方程的根与函数图象交点之间的转化问题,考查了数形结合思想,推理能力与计算能力,属于难题.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{25}{36}$ | D. | $\frac{11}{36}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$+1 | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | 2 | D. | $\frac{{1+\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
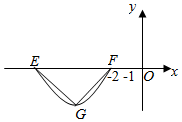 偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,其中△EFG是斜边为4的等腰直角三角形(E、F是函数图象与x轴的交点,点G在图象上),则f(1)的值为( )
偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,其中△EFG是斜边为4的等腰直角三角形(E、F是函数图象与x轴的交点,点G在图象上),则f(1)的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com