
 如图,在平行四边形ABCD中,AH=HB,DF=MC=$\frac{1}{4}$DC,若$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}$=$\overrightarrow b$,试用$\overrightarrow a,\overrightarrow b$分别表示$\overrightarrow{AM},\overrightarrow{MH},\overrightarrow{AF}$.
如图,在平行四边形ABCD中,AH=HB,DF=MC=$\frac{1}{4}$DC,若$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}$=$\overrightarrow b$,试用$\overrightarrow a,\overrightarrow b$分别表示$\overrightarrow{AM},\overrightarrow{MH},\overrightarrow{AF}$. 分析 利用向量的平行四边形法则求解即可.
解答 解:在平行四边形ABCD中,AH=HB,DF=MC=$\frac{1}{4}$DC,可知AHMF是平行四边形,
$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}$=$\overrightarrow b$,
可得$\overrightarrow{AF}$=$\overrightarrow{AD}$+$\overrightarrow{DF}$=$\overrightarrow{b}+\frac{1}{4}\overrightarrow{a}$,
$\overrightarrow{MH}=-\overrightarrow{AF}$=$-\overrightarrow{b}-\frac{1}{4}\overrightarrow{a}$.
$\overrightarrow{AM}$=$\overrightarrow{AH}+\overrightarrow{AF}$=$\frac{1}{2}\overrightarrow{a}+\overrightarrow{b}+\frac{1}{4}\overrightarrow{a}$=$\overrightarrow{b}+\frac{3}{4}\overrightarrow{a}$.
点评 本题考查向量的平行四边形法则的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | -$\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
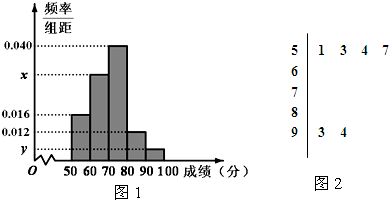 为选拔选手参加“中国汉字听写大会”,某中学举行了一次“汉字听写大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
为选拔选手参加“中国汉字听写大会”,某中学举行了一次“汉字听写大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com