
分析 直线l1:y=2x与直线l2:ax+by+c=0(abc≠0)相互垂直,可得2×(-$\frac{a}{b}$)=-1,化为b=2a.当a,b,c成等差数列时,2b=a+c.由ax+by+c=0(abc≠0),令x=0,解得y.联立$\left\{\begin{array}{l}{y=2x}\\{ax+by+c=0}\end{array}\right.$,解得x=$\frac{-c}{a+2b}$.即可直线l1,l2与y轴围成的三角形的面积S.
解答 解:直线l1:y=2x与直线l2:ax+by+c=0(abc≠0)相互垂直,∴2×(-$\frac{a}{b}$)=-1,化为b=2a.
当a,b,c成等差数列时,2b=a+c.
∴b=2a,c=3a.
由ax+by+c=0(abc≠0),令x=0,解得y=-$\frac{c}{b}$.
联立$\left\{\begin{array}{l}{y=2x}\\{ax+by+c=0}\end{array}\right.$,解得x=$\frac{-c}{a+2b}$.
直线l1,l2与y轴围成的三角形的面积S=$\frac{1}{2}×|\frac{-c}{a+2b}|$×$|\frac{-c}{b}|$=$\frac{1}{2}×|\frac{9{a}^{2}}{5a×2a}|$=$\frac{9}{20}$.
故答案为:$\frac{9}{20}$.
点评 本题考查了直线垂直与斜率之间的关系、等差数列的性质、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:解答题
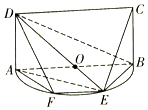 如图,半圆O的直径AB长为2,E是半圆O上除A,B外的一个动点,矩形ABCD所在的平面垂直于该半圆所在的平面,且$tan∠DBA=\frac{1}{2}$,设平面ECD与半圆弧的另一个交点为F.
如图,半圆O的直径AB长为2,E是半圆O上除A,B外的一个动点,矩形ABCD所在的平面垂直于该半圆所在的平面,且$tan∠DBA=\frac{1}{2}$,设平面ECD与半圆弧的另一个交点为F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com