
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
| 7 |
| 6 |
| 2π |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 =(
=( cosωx,sinωx),
cosωx,sinωx), =(sinωx,0),其中ω>0,记函数f(x)=(
=(sinωx,0),其中ω>0,记函数f(x)=( +
+ )•
)• +k.
+k. ,求ω的取值范围;
,求ω的取值范围; ,
, ]时,函数f(x)的最大值是
]时,函数f(x)的最大值是 ,求函数f(x)的解析式,并说明如何由函数y=sinx的图象变换得到函数y=f(x)的图象.
,求函数f(x)的解析式,并说明如何由函数y=sinx的图象变换得到函数y=f(x)的图象.查看答案和解析>>
科目:高中数学 来源: 题型:
(08年莆田四中二模文)给出下列四个结论:
①函数![]() 在其各自
在其各自
定义域上具备相同单调性;
②函数![]() 为非零常数)的图象可由函数y=3x的图象经过平移得到;
为非零常数)的图象可由函数y=3x的图象经过平移得到;
③函数![]() 是偶函数;
是偶函数;
④函数y=cos|x|是周期函数.
其中正确结论的序号是 .(填写你认为正确的所有结论序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
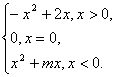
(1)求实数m的值,并在直角坐标系中画出y=f(x)的图象;
(2)若函数f(x)在区间[-1,|a|-2]上单调递增,试确定a的取值范围.
(文)设函数f(x)=(![]() sinωx+cosωx)cosωx(其中0<ω<2).
sinωx+cosωx)cosωx(其中0<ω<2).
(1)若f(x)的周期为π,求当-![]() ≤x≤
≤x≤![]() 时,f(x)的值域;
时,f(x)的值域;
(2)若函数f(x)的图象的一条对称轴方程为x=![]() ,求ω的值.
,求ω的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com