练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    (理)已知奇函数f(x)=

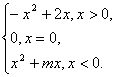
    (1)求实数m的值,并在直角坐标系中画出y=f(x)的图象;

    (2)若函数f(x)在区间［-1,|a|-2］上单调递增,试确定a的取值范围.

    (文)设函数f(x)=(sinωx+cosωx)cosωx(其中0＜ω＜2).

    (1)若f(x)的周期为π,求当-≤x≤时,f(x)的值域;

    (2)若函数f(x)的图象的一条对称轴方程为x=,求ω的值.

    答案：(理)解:(1)当x＜0时,-x＞0,f(-x)=-(-x)2+2(-x)=-x2-2x.

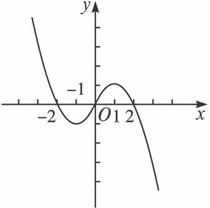
    又f(x)为奇函数,∴f(-x)=-f(x)=-x2-2x.∴f(x)=x2+2x.∴m=2.y=f(x)的图象如上图所示.

    (2)由(1)知f(x)=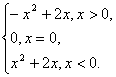由图象可知,f(x)在[-1,1]上单调递增,要使f(x)在[-1,|a|-2]上单调递增,只需解之,得-3≤a＜-1或1＜a≤3.

    (文)解:f(x)=sinωxcosωx+cos2ωx=sin2ωx+=sin(2ωx+)+.

    (1)f(x)周期为π,∴=π.∴ω=1.∴f(x)=sin(2x+)+.∵-≤x≤,∴-≤2x+≤.

    ∴-≤sin(2x+)≤1.∴0≤f(x)≤.

    (2)令2ωx+=kπ+(k∈Z),得ωx=+(k∈Z).当x=时,得ω=(k∈Z),0＜ω＜2且k∈Z,∴k=0.∴ω=.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （文）已知奇函数f（x）满足f（x+3）=f（x），当x∈（0，1）时，函数f（x）=3x-1，则f(log
    1
    3
    36)    =
     

    （理）已知点G是△ABC的重心，O是空间任意一点，若
    OA
    +
    OB
    +
    OC
    =λ
    OG
    ，则λ的值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•奉贤区二模）（理）已知函数f(x)=
    .
    sinxcosx
    -sinαcosα
    .
    ，g(x)=
    .
    cosxsinx
    sinβcosβ
    .
    ，α，β是参数，x∈R，α∈(-
    π
    2
    ，
    π
    2
    )    ，β∈(-
    π
    2
    ，
    π
    2
    )
    （1）若α=
    π
    4
    ，β=
    π
    4
    ，判别h（x）=f（x）+g（x）的奇偶性；
    若α=-
    π
    4
    ，β=
    π
    4
    ，判别h（x）=f2（x）+g2（x）的奇偶性；
    （2）若α=
    π
    3
    ，t（x）=f（x）g（x）是偶函数，求β；
    （3）请你仿照问题（1）（2）提一个问题（3），使得所提问题或是（1）的推广或是问题（2）的推广，问题（1）或（2）是问题（3）的特例．（不必证明命题）
    将根据写出真命题所体现的思维层次和对问题探究的完整性，给予不同的评分．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    （文）已知奇函数f（x）满足f（x+3）=f（x），当x∈（0，1）时，函数f（x）=3x-1，则数学公式=________
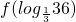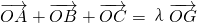    （理）已知点G是△ABC的重心，O是空间任意一点，若数学公式，则λ的值是________．

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年江西省吉安市白鹭洲中学高二（上）期中数学试卷（解析版） 题型：填空题

    （文）已知奇函数f（x）满足f（x+3）=f（x），当x∈（0，1）时，函数f（x）=3x-1，则=   
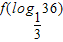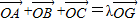    （理）已知点G是△ABC的重心，O是空间任意一点，若，则λ的值是    ．

    查看答案和解析>>

    同步练习册答案