
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2, AD=CD=,PA=,∠ABC=120°,G为线段PC上的点

(1)证明:BD⊥面PAC
(2)若G是PC的中点,求DG与APC所成的角的正切值
(3)若G满足PC⊥面BGD,求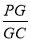 的值.
的值.
【解析】
(1)证明:∵在四棱锥P﹣ABCD中,PA⊥面ABCD,∴PA⊥BD.
∵AB=BC=2,AD=CD=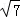 ,设AC与BD的交点为O,则BD是AC的中垂线,故O为AC的中点,且BD⊥AC.
,设AC与BD的交点为O,则BD是AC的中垂线,故O为AC的中点,且BD⊥AC.
而PA∩AC=A,∴BD⊥面PAC.
(2)若G是PC的中点,O为AC的中点,则GO平行且等于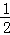 PA,故由PA⊥面ABCD,可得GO⊥面ABCD,
PA,故由PA⊥面ABCD,可得GO⊥面ABCD,
∴GO⊥OD,故OD⊥平面PAC,故∠DGO为DG与平面PAC所成的角.
由题意可得,GO=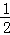 PA=
PA=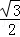 .
.
△ABC中,由余弦定理可得AC2=AB2+BC2﹣2AB•BC•cos∠ABC=4+4﹣2×2×2×cos120°=12,
∴AC=2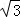 ,OC=
,OC=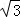 .
.
∵直角三角形COD中,OD=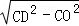 =2,
=2,
∴直角三角形GOD中,tan∠DGO=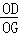 =
=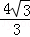 .
.
(3)若G满足PC⊥面BGD,∵OG?平面BGD,∴PC⊥OG,且 PC=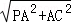 =
=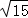 .
.
由△COG∽△CAP,可得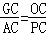 ,即
,即 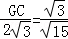 ,解得GC=
,解得GC=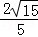 ,
,
∴PG=PC﹣GC=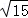 ﹣
﹣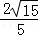 =
=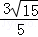 ,∴
,∴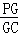 =
=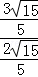 =
=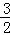 ..
..
【解析】
试题分析:(1)利用直线和平面垂直的判定定理证得BD⊥面PAC.
(2)由三角形的中位线性质以及条件证明∠DGO为DG与平面PAC所成的角,求出GO和AC的值,可得OC、OD的值,再利用直角三角形中的边角关系求得tan∠DGO的值.
(3)由△COG∽△CAP,可得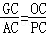 ,解得GC的值,可得PG=PC﹣GC 的值,从而求得
,解得GC的值,可得PG=PC﹣GC 的值,从而求得 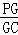 的值.
的值.
考点:直线与平面垂直的判定;直线与平面所成的角.


科目:高中数学 来源:2014-2015学年北京市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
将函数 的图象向左平移
的图象向左平移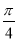 个单位,再向上平移1个单位,所得图象的函数解析式是( )
个单位,再向上平移1个单位,所得图象的函数解析式是( )
(A)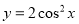 (B)
(B)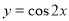
(C)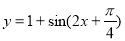 (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年安徽省淮北市高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
已知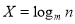 ,则
,则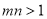 是
是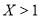 的( )。
的( )。
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年天津市高三上学期第二次月考文科数学试卷(解析版) 题型:选择题
定义行列式运算 =
= .将函数
.将函数 的图象向左平移
的图象向左平移 个单位,以下是所得函数图象的一个对称中心是( )
个单位,以下是所得函数图象的一个对称中心是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年贵州省高三模拟考试文科数学试卷(解析版) 题型:选择题
已知函数 是定义在
是定义在 上的增函数,函数
上的增函数,函数 的图像关于点
的图像关于点 对称,
对称,
若任意的 、
、 ,不等式
,不等式 恒成立,则当
恒成立,则当 时,
时, 的
的
取值范围是
A.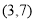 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷(解析版) 题型:填空题
(2003•北京)如图,已知底面半径为r的圆柱被一个平面所截,剩下部分母线长的最大值为a,最小值为b,那么圆柱被截后剩下部分的体积是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com