
| A. | 命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0,则x=1” | |
| B. | 若p∨q为真命题,则p、q均为真命题 | |
| C. | 若命题p:?x∈R,x2+x+1≠0,则?p:?x∈R,x2+x+1=0 | |
| D. | a,b,c∈R,则“ac2>bc2”是“a>b”的充分不必要条件 |
分析 由逆否命题的变换形式知A选项正确,对于B选项,若p∨q为真命题,则命题p、q中至少有一个是真命题,故B选项错误,由全称命题的否定知C选项正确,由充分必要条件的定义,可判断D正确.
解答 解:A.命题“若x≠1,则x2-3x+2≠0”的逆否命题是“若x2-3x+2=0则x=1”,故A正确;
B.若p∨q为真命题,则p,q至少有一个为真命题,故B错误;
C.若命题p::?x∈R,x2+x+1≠0,则¬p:?x∈R,x2+x+1=0,故C正确;
D.若a,b,c∈R,则“ac2>bc2”,∴c≠0,∴a>b,充分性成立;反之,“a>b”不能推出“ac2>bc2”,如c2=0,则ac2=bc2,即必要性不成立,故D正确.
故选:B.
点评 本题考查四种命题及真假,命题的否定,以及复合命题的真假,充分必要条件的判断,属于基础题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-1,\frac{1}{3}$ | B. | $1,\frac{2}{3}$ | C. | $1,\frac{1}{3}$ | D. | $1,\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
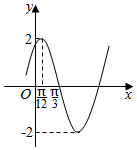 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列说法中,所有正确说法的序号是①②
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列说法中,所有正确说法的序号是①②查看答案和解析>>
科目:高中数学 来源: 题型:解答题
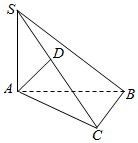 已知△ABC中∠ACB=90°,SA⊥面ABC,AD⊥SC,
已知△ABC中∠ACB=90°,SA⊥面ABC,AD⊥SC,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}+1}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com