
 ��֪����f��x��=Asin����x+�գ���A��0���أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ��������˵���У�������ȷ˵��������Ǣ٢�
��֪����f��x��=Asin����x+�գ���A��0���أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ��������˵���У�������ȷ˵��������Ǣ٢����� ����������Ľ���ʽ���ٽ�Ϻ�����ͼ������жϣ����ɵó����ۣ�
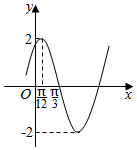
��� �⣺�����⣬A=2��$\frac{T}{4}$=$\frac{��}{3}-\frac{��}{12}$=$\frac{��}{4}$�����=2��
��$\frac{��}{12}$��2�����뺯�����ɵæ�=$\frac{��}{3}$����f��x��=2sin��2x+$\frac{��}{3}$����
������Ϊ�У�f��x����ͼ�����ֱ��x=$\frac{��}{12}$�Գƣ��ɵ�f��x����ͼ�����ֱ��x=$\frac{7��}{12}$�Գƣ���ȷ
����ͼ��ɵ�f��x���ĵ�����������Ϊ[k��-$\frac{5��}{12}$��k��+$\frac{��}{12}$]��k��Z����ȷ��
�۷���f��x��=1��[-$\frac{��}{2}$��0]����1��ʵ��������ȷ��
�ܺ���f��x����ͼ�����ɺ���y=2sin��2x-$\frac{��}{6}$����ͼ������ƽ��$\frac{��}{4}$����λ�õ��ģ�����ȷ��
�ʴ�Ϊ���٢ڣ�
���� ���⿼�����Һ�����ͼ�������ʣ��������ν�ϵ���ѧ˼�룬����ѧ�������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{1}{2}$ | C�� | $\frac{1}{3}$ | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{��}$ | B�� | $\frac{��}{2}$ | C�� | ��-2 | D�� | $\frac{2}{��}$��$\frac{��}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֱ�Ҫ���� | B�� | ��ֲ���Ҫ���� | ||
| C�� | ��Ҫ��������� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���⡰��x��1����x2-3x+2��0������������ǡ���x2-3x+2=0����x=1�� | |
| B�� | ��p��qΪ�����⣬��p��q��Ϊ������ | |
| C�� | ������p��?x��R��x2+x+1��0����?p��?x��R��x2+x+1=0 | |
| D�� | a��b��c��R����ac2��bc2���ǡ�a��b���ij�ֲ���Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com