
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
分析 对m分类讨论,利用两条直线相互垂直的充要条件即可得出.
解答 解:分类讨论:当m=1时,直线l1的斜率不存在,直线l2的斜率为0,此时两条直线相互垂直.
当m=-$\frac{3}{2}$时,直线l1的斜率存在为-$\frac{3}{5}$,直线l2的斜率不存在,此时两条直线不垂直,舍去.
当m≠-$\frac{3}{2}$,1时,由两条直线相互垂直,可得:$-\frac{m}{1-m}$×($-\frac{m-1}{2m+3}$)=-1,解得m=-3.
综上可得:m=-3或1时两条直线相互垂直,
因此:“m=-3”是“直线l1:mx+(1-m)y-3=0与直线l2:(m-1)x+(2m+3)y-2=0相互垂直”的充分不必要条件.
故选:B.
点评 本题考查了直线相互垂直与斜率之间的关系、简易逻辑的判定方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,-1)∪(1,+∞) | C. | (-∞,-1)∪[1,+∞) | D. | (-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
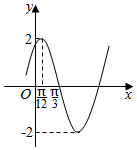 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列说法中,所有正确说法的序号是①②
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列说法中,所有正确说法的序号是①②查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com