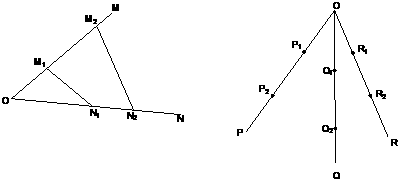
解:(1)如图,4条直线有5个交点,
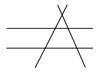
故f(4)=5,
由f(3)=2,
f(4)=f(3)+3
…
f(n-1)=f(n-2)+n-2
f(n)=f(n-1)+n-1
累加可得f(n)=2+3+…+(n-2)+(n-1)
=
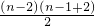
=
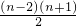
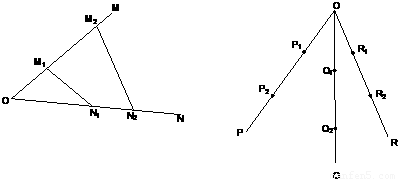
(2)如图,过R
2作R
2M
2⊥平面P
2OQ
2于M
2,连OM
2.过R
1在平面OR
2M
2作R
1M
1∥R
2M
2交OM
2于M
1,
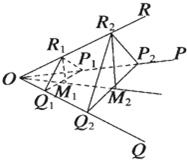
则R
1M
1⊥平面P
2OQ
2.
由
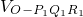
=

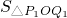
•R
1M
1=

•

OP
1•OQ
1•sin∠P
1OQ
1•R
1M
1=

OP
1•OQ
1•R
1M
1•sin∠P
1OQ
1,
同理,
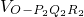
=

OP
2•OQ
2•R
2M
2•sin∠P
2OQ
2.
∴
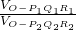
=
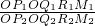
.
由平面几何知识可得
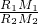
=
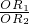
.
∴
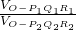
=
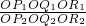
.
故答案为(1)5,
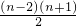
(2)
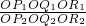
.
分析:(1)要想求出f(4)的值,我们画图分析即可得到答案,但要求出n>4时f(n)的值,我们要逐一给出f(3),f(4),…,f(n-1),f(n)然后分析项与项之间的关系,然后利用数列求和的办法进行求解.
(2)由平面图形中点的性质类比推理出空间里的线的性质,由平面图形中线的性质类比推理出空间中面的性质,由平面图形中面的性质类比推理出空间中体的性质.
点评:本题考查的知识点是推理,其中(1)是归纳推理,根据f(3),f(4),…,f(n-1),f(n)然后分析项与项之间的关系,找出项与项之间的变化趋势是解决问题的关键;(2)是类比推理,一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

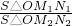 =
=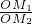 =
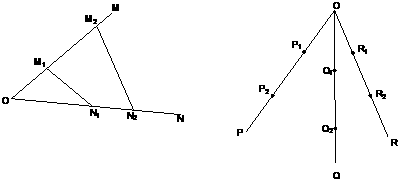
=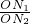 ,若不在同一平面内的射线OP,OQ和OR上分别存在点P1P2,点Q1Q2和点R1R2,则
,若不在同一平面内的射线OP,OQ和OR上分别存在点P1P2,点Q1Q2和点R1R2,则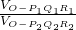 =________.
=________.

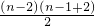
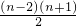

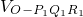 =
=
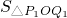 •R1M1=
•R1M1= •
• OP1•OQ1•sin∠P1OQ1•R1M1
OP1•OQ1•sin∠P1OQ1•R1M1 OP1•OQ1•R1M1•sin∠P1OQ1,
OP1•OQ1•R1M1•sin∠P1OQ1,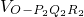 =
= OP2•OQ2•R2M2•sin∠P2OQ2.
OP2•OQ2•R2M2•sin∠P2OQ2.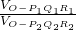 =
=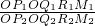 .
.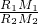 =
=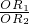 .
.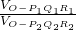 =
=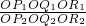 .
.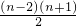
 .
.

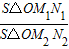 =
=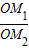 =
=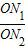 ,若不在同一平面内的射线OP,OQ和OR上分别存在点P1P2,点Q1Q2和点R1R2,则
,若不在同一平面内的射线OP,OQ和OR上分别存在点P1P2,点Q1Q2和点R1R2,则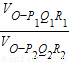 =______.
=______.