
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 与圆
与圆![]() 外切于原点
外切于原点![]() ,且两圆圆心的距离
,且两圆圆心的距离![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求圆![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)过点![]() 的直线
的直线![]() ,
,![]() 与圆
与圆![]() 异于点
异于点![]() 的交点分别为点
的交点分别为点![]() ,
,![]() ,与圆
,与圆![]() 异于点
异于点![]() 的交点分别为点
的交点分别为点![]() ,
,![]() ,且
,且![]() ,求四边形面积
,求四边形面积![]() 的最大值.
的最大值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】对于定义城为R的函数![]() ,若满足:①
,若满足:①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() 且
且![]() 时,都有
时,都有![]() ,则称
,则称![]() 为“偏对称函数”.下列函数是“偏对称函数”的是( )
为“偏对称函数”.下列函数是“偏对称函数”的是( )
A.![]() B.
B.![]()
C.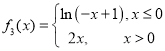 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
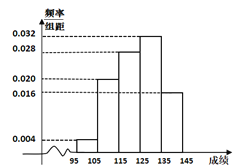
【题目】半期考试后,班长小王统计了50名同学的数学成绩,绘制频率分布直方图如图所示.
![]() 根据频率分布直方图,估计这50名同学的数学平均成绩;
根据频率分布直方图,估计这50名同学的数学平均成绩;
![]() 用分层抽样的方法从成绩低于115的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学数学成绩均在
用分层抽样的方法从成绩低于115的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学数学成绩均在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的右焦点为F,点A(一2,2)为椭圆C内一点。若椭圆C上存在一点P,使得|PA|+|PF|=8,则m的取值范围是( ).
的右焦点为F,点A(一2,2)为椭圆C内一点。若椭圆C上存在一点P,使得|PA|+|PF|=8,则m的取值范围是( ).
A. ![]() B. [9,25] C.
B. [9,25] C. ![]() D. [3,5]
D. [3,5]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,分别从两厂随机各选取了![]() 个轮胎,将每个轮胎的宽度(单位:
个轮胎,将每个轮胎的宽度(单位: ![]() )记录下来并绘制出如下的折线图:
)记录下来并绘制出如下的折线图:
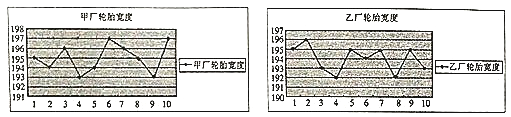
(1)分别计算甲、乙两厂提供的![]() 个轮胎宽度的平均值;
个轮胎宽度的平均值;
(2)轮胎的宽度在![]() 内,则称这个轮胎是标准轮胎.
内,则称这个轮胎是标准轮胎.
(i)若从甲乙提供的![]() 个轮胎中随机选取
个轮胎中随机选取![]() 个,求所选的轮胎是标准轮胎的概率
个,求所选的轮胎是标准轮胎的概率![]() ;
;
(ii)试比较甲、乙两厂分别提供的![]() 个轮胎中所有标准轮胎宽度的方差大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好?
个轮胎中所有标准轮胎宽度的方差大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com