
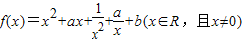 .若实数a、b使得f(x)=0有实根,则a2+b2的最小值为( )
.若实数a、b使得f(x)=0有实根,则a2+b2的最小值为( )

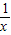 =t进而可知t的范围,要使f(x)=0有实根需判别式大于等于0且小根小于-2或大根大于2,进而根据韦达定理确定a和b的范围,求得f(t)=t2+at+b-2=0的,根据t的范围确定:±
=t进而可知t的范围,要使f(x)=0有实根需判别式大于等于0且小根小于-2或大根大于2,进而根据韦达定理确定a和b的范围,求得f(t)=t2+at+b-2=0的,根据t的范围确定:±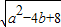 =2t+a≥ta+b+k2-2=0则a2+b2的最小值即为原点到该直线的距离的平方,进而根据d(t)的范围求得a2+b2的最小值.
=2t+a≥ta+b+k2-2=0则a2+b2的最小值即为原点到该直线的距离的平方,进而根据d(t)的范围求得a2+b2的最小值.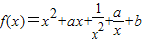 =(x+
=(x+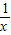 )2+a(x+
)2+a(x+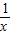 )+b-2
)+b-2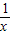 =t,则t≥2或t≤-2
=t,则t≥2或t≤-2 (a±
(a±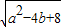 ),则|t|≥2.
),则|t|≥2.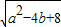 =2t+a≥ta+b+k2-2=0
=2t+a≥ta+b+k2-2=0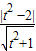 ≥d2(t)=t2-5+
≥d2(t)=t2-5+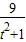 ≥d2(t)min=
≥d2(t)min= ,当|t|=2时,等号成立.
,当|t|=2时,等号成立.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012-2013学年辽宁省丹东市宽甸二中高一(上)期末数学试卷(解析版) 题型:解答题
 ,若实数a满足f(a)<0,且f[f(a)]=1,求a的值.
,若实数a满足f(a)<0,且f[f(a)]=1,求a的值.查看答案和解析>>
科目:高中数学 来源:2011年四川省成都七中高考数学三模试卷(理科)(解析版) 题型:选择题
 ,若实数a使得f(x)=0有实根,则a的最大值是( )
,若实数a使得f(x)=0有实根,则a的最大值是( )

查看答案和解析>>
科目:高中数学 来源:2007年北京市海淀区高考数学一模试卷(理科)(解析版) 题型:选择题
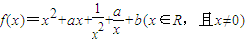 .若实数a、b使得f(x)=0有实根,则a2+b2的最小值为( )
.若实数a、b使得f(x)=0有实根,则a2+b2的最小值为( )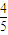

查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省广州市执信中学高三(下)2月月考数学试卷(理科)(解析版) 题型:选择题
 ,若实数a,b满足f(a)+f(b-2)=0,则a+b=( )
,若实数a,b满足f(a)+f(b-2)=0,则a+b=( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com