
已知点P、Q分别为函数y=ln(x—1)+1和y=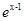 +1图像上的动点,O为坐标原点,当1PQ1最小时,直线OQ交函数y=
+1图像上的动点,O为坐标原点,当1PQ1最小时,直线OQ交函数y=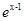 +1的图像于点R(
+1的图像于点R( ,
,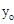 )(异于Q点),则
)(异于Q点),则 =
=
A.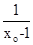 B.
B.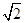 C.2 D.3
C.2 D.3
 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
| OQ |
| m |
| OP |
| n |
| m |
| 1 |
| 2 |
| n |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2004年高考北京四中全真模拟试卷——数学 题型:013
已知点P(t,m)是函数y=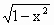 图象上的动点,过点P作此函数图象的切线,切线斜率k是点P横坐标t的函数,记为k=f(t),则函数k=f(t)在(-1,1)上是
图象上的动点,过点P作此函数图象的切线,切线斜率k是点P横坐标t的函数,记为k=f(t),则函数k=f(t)在(-1,1)上是
[ ]
A.单调递增函数
B.单调递减函数
C.(-1,0]上增函数,在[0,1)上减函数.
D.(-1,0]上减函数,在[0,1)上增函数.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏五校高三下学期期初教学质量调研数学卷(解析版) 题型:填空题
若点P、Q分别在函数y=ex和函数 y=lnx的图象上,则P、Q两点间的距离的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
直三棱柱ABC——A1B1C1的体积为V,已知点P、Q分别为AA1、CC1上的点,而且满足AP=C1Q,则四棱锥B—APQC的体积是( )
A、 ![]() V B、
V B、 ![]() V C、
V C、 ![]() V D、
V D、 ![]() V
V
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com