练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    △ABC中，A=
    π
    3
    ，AB=3，AC=8，则BC=
     
    ．
    考点：余弦定理
    专题：解三角形
    分析：△ABC中，由余弦定理可得，BC2=AB2+AC2-2AB•ACcosA可求BC．
    解答： 解：由余弦定理可得，BC2=AB2+AC2-2AB•ACcosA
    =9+64+9-2×3×8cos60°=49，
    ∴BC=7，
    故答案为：7．
    点评：本题主要考查了利用余弦定理解三角形，属于公式的基本应用，是基础题目．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

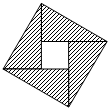    三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示，我们教材中利用该图作为“（　　）”的几何解释．
    A、如果a＞b，b＞c，那么a＞c
    B、如果a＞b＞0，那么a2＞b2
    C、对任意实数a和b，有a2+b2≥2ab，当且仅当a=b时等号成立
    D、如果a＞b，c＞0那么ac＞bc

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知集合A={x∈N|x＜6}，则下列关系式错误的是（　　）
    A、0∈AB、1.5∉A
    C、-1∉AD、6∈A

    查看答案和解析>>

    科目：高中数学 来源： 题型：

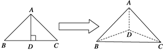    如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，则下列四个结论中错误的是（　　）
    A、BD⊥AC
    B、△ABC是等边三角形
    C、平面ADC⊥平面ABC
    D、二面角A-BC-D的正切值为
    		2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，三棱柱的侧棱长为2，底面是边长为2的正三角形，AA1⊥面A1B1C1，正视图是边长为2正方形．
    （Ⅰ）求侧视图的面积；
    （Ⅱ）求直线AC1与平面BB1C1C所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=lnx-x+a有且只有一个零点．
    （1）求a的值；
    （2）若对任意的x∈（1，+∞），有2f（x）＜
    k
    x
    -x+2恒成立，求实数k的最小值；
    （3）设h（x）=f（x）+x-1，对任意x1，x2∈（0，+∞）（x1≠x2），证明：不等式
    x1-x2
    h(x1)-h(x2)
    ＞
    		x1x2
    恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）当x趋近于x0时极限存在是f（x）在点x0的某个去心领域内有界的（　　）
    A、充分不必要条件
    B、必要不充分条件
    C、充分必要条件
    D、即不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，空间四边形ABCD中，各边及对角线长均为2，E是AB的中点，过CE且平行于AD的平面交BD于F，则△CEF的面积为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    数列{an}中，a1=2，an+1=
    2an
    4+an
    （n∈N*），求数列{an}的通项公式．

    查看答案和解析>>

    同步练习册答案