

剖析:本题考查相互独立事件同时发生和互斥事件有一个发生的概率的计算方法,考查运用概率知识解决实际问题的能力.正确理解相互独立事件与互斥事件,掌握相互独立事件概率的乘法公式是解决本题的关键.
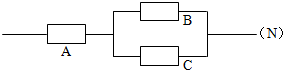
解:分别记元件A、B、C正常工作为事件A、B、C,由已知条件知
P(A)=0.80,P(B)=0.90,P(C)=0.90.
(1)因为事件A、B、C是相互独立的,所以,系统N1正常工作的概率
P1=P(ABC)=P(A)P(B)P(C)
=0.80×0.90×0.90=0.648.
故系统N1正常工作的概率为0.648.
(2)系统N2正常工作的概率
P2=P(A)[1-P(![]() )]
)]
=P(A)[1-P(![]() )P(
)P(![]() )],
)],
∵P(![]() )=1-P(B)=1-0.90=0.10,
)=1-P(B)=1-0.90=0.10,
P(![]() )=1-P(C)=1-0.90=0.10,
)=1-P(C)=1-0.90=0.10,
∴P2=0.80×[1-0.10×0.10]
=0.80×0.99=0.792.
故系统N2正常工作的概率为0.792.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记
如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记| AB |
| a |
| AC |
| b |
| AA |
| c |
| DE |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:
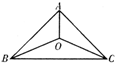 三个城市分别位于A,B,C三点处(如图),且AB=AC=20
三个城市分别位于A,B,C三点处(如图),且AB=AC=20| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 斜三棱柱OAB-CA1B1,其中向量
斜三棱柱OAB-CA1B1,其中向量| OA |
| a |
| OB |
| b |
| OC |
. |
| c |
| π |
| 3 |
| CM |
| 1 |
| 2 |
| MA1 |
| BN |
| NA1 |
| OA |
| OB |
| |OC| |
| AM |
| a |
| c |
| AM |
| ON |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com