
(本小题12分)设函数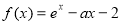 .
.
(1)求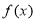 的单调区间;
的单调区间;
(2)若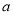 =1 ,
=1 ,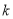 为整数,且当
为整数,且当
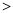 0时,
0时,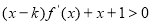 ,求
,求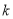 的最大值.
的最大值.
(1)若 ,则
,则 ,此时函数
,此时函数 在R上单调递增;
在R上单调递增;
若 ,则当
,则当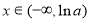 时,
时, ;当
;当 时,
时, .所以函数
.所以函数 在
在 上单调递减;在
上单调递减;在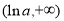 上单调递增.
上单调递增.
(2)整数 的最大值为2.
的最大值为2.
【解析】
试题分析:(1)首先根据函数 的表达式可判断其定义域,然后对其进行求导可得
的表达式可判断其定义域,然后对其进行求导可得 ,由于导函数中含有参数
,由于导函数中含有参数 ,将其分为两种情况:①
,将其分为两种情况:① ,此时易判断出函数
,此时易判断出函数 在R上单调递增;②
在R上单调递增;② ,可求出其极值点,然后判断函数在极值点的左右两侧的单调性即可;
,可求出其极值点,然后判断函数在极值点的左右两侧的单调性即可;
(2)首先将问题“当
 0时,
0时, ”转化为“
”转化为“ 恒成立,其中
恒成立,其中 ”,即
”,即 ,记
,记 ,求其导函数
,求其导函数 ,由(1)知,函数
,由(1)知,函数 在
在 上单调递增,且在
上单调递增,且在 上存在唯一的零点,即
上存在唯一的零点,即 在
在 上存在唯一的零点.从而得出函数
上存在唯一的零点.从而得出函数 的最小值并求出其取值范围,进而得出整数
的最小值并求出其取值范围,进而得出整数 的最大值.
的最大值.
试题解析:(1)函数 的定义域为R,所以
的定义域为R,所以 .
.
若 ,则
,则 ,此时函数
,此时函数 在R上单调递增;
在R上单调递增;
若 ,则当
,则当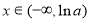 时,
时, ;当
;当 时,
时, .所以函数
.所以函数 在
在 上单调递减;在
上单调递减;在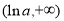 上单调递增.
上单调递增.
(2)因为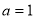 ,所以
,所以 ,所以当
,所以当 时,
时, 等价于
等价于 ,其中
,其中 .
.
令 ,则
,则 .
.
由(1)知,函数 在
在 上单调递增,而
上单调递增,而 ,
, ,所以
,所以 在
在 上存在唯一的零点,故
上存在唯一的零点,故 在
在 上存在唯一的零点.设此零点为
上存在唯一的零点.设此零点为 ,则
,则 .
.
当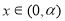 时,
时, ;当
;当 时,
时, ;所以
;所以 在
在 上的最小值为
上的最小值为 .又由
.又由 可得,
可得, ,所以
,所以 ,所以
,所以 ,故整数
,故整数 的最大值为2.
的最大值为2.
考点:1、利用导数判断函数的单调性;2、导数在研究函数的最值中的应用.


科目:高中数学 来源:2015届辽宁省五校协作体高三上学期期中考试文科数学试卷(解析版) 题型:选择题
设l为直线,?,?是两个不同的平面,下列命题中正确的是( )
A.若 ,
, ,则
,则
B.若 ,
, ,则
,则
C.若 ,
, ,则
,则
D.若 ,
, ,则
,则
查看答案和解析>>
科目:高中数学 来源:2015届西藏拉萨中学高三第三次月考文科数学试卷(解析版) 题型:选择题
已知数列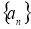 是等比数列,
是等比数列, 是其前
是其前 项和,且
项和,且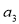 =2,
=2,  ,则
,则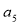 =
=
A.2或- B.
B.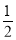 或-2 C.
或-2 C. D.2或
D.2或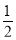
查看答案和解析>>
科目:高中数学 来源:2015届福建省福州市高三上学期第三次质检理科数学试卷(解析版) 题型:填空题
直线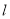 与函数
与函数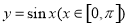 的图像相切于点
的图像相切于点 ,且
,且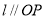 ,
, 为坐标原点,
为坐标原点,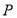 为图像的极大值点,
为图像的极大值点,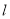 与
与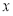 轴交于点
轴交于点 ,过切点
,过切点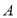 作
作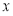 轴的垂线,垂足为
轴的垂线,垂足为 ,则
,则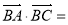 =__________.
=__________.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高三10月月考理科数学试卷(解析版) 题型:解答题
(本小题满分13分)某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和厢期会因供应不足使价格呈
持续上涨态势,而中期又将出现供大于求使价格连续下跌.现有三种价格模拟函数:①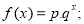 ②
②
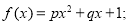 ③
③ (以上三式中
(以上三式中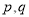 均为常数,且q>l).
均为常数,且q>l).
(1)为准确研究其价格走势,应选哪种价格模拟函数(不必说明理由);
(2)若 ,求出所选函数
,求出所选函数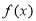 的解析式(注:函数定义域是
的解析式(注:函数定义域是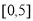 .其中
.其中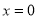 表示8
表示8
月1日,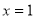 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);
(3)在(2)的条件下研究下面课题:为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com