Question

18．已知函数f（x）=ax²+2bx+c．
（Ⅰ）若a=-1，c=0，且y=f（x）在[-1，3]上的最大值为g（b），求g（b）；
（Ⅱ）若a=1，且f（x）在区间（1，2）内有且仅有2个零点，求证：0＜b+c＜2．

Answer 1

分析 （Ⅰ）求出a=-1，c=0时的f（x）解析式，配方求出对称轴，讨论区间[-1，3]与对称轴的关系，运用单调性即可得到最大值g（b）；
（Ⅱ）由题意可得判别式大于0，对称轴介于（1，2），f（1）＞0，f（2）＞0，作出不等式组表示的区域，再由直线b+c=0平移可得最值，进而得到所求范围．

解答 解：（Ⅰ）a=-1，c=0时，f（x）=-x²+2bx=-（x-b）²+b²，
∴对称轴是直线x=b，
①b＜-1时，[-1，3]为减区间，即有f（x）_max=f（-1）=-1-2b；
②当-1≤b≤3时，即有f（x）_max=g（b）=b²；
③当b＞3时，[-1，3]为增区间，即有f（x）_max=f（3）=-9+6b．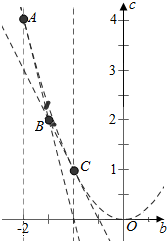
综上所述，g（b）=$\left\{\begin{array}{l}{-1-2b，b＜-1}\\{{b}^{2}，-1≤b≤3}\\{6b-9，b＞3}\end{array}\right.$； 
（Ⅱ）证明：若a=1即有f（x）=x²+2bx+c，
f（x）在区间（1，2）内有且仅有2个零点，
可得$\left\{\begin{array}{l}{△=4{b}^{2}-4c＞0}\\{1＜-b＜2}\\{1+2b+c＞0}\\{4+4b+c＞0}\end{array}\right.$，即有$\left\{\begin{array}{l}{{b}^{2}＞c}\\{-2＜b＜-1}\\{2b+c＞-1}\\{4b+c＞-4}\end{array}\right.$，
作出不等式组表示的可行域，（以b为x轴，c为y轴），
求得A（-2，4），C（-1，1），B（-$\frac{3}{2}$，2），
即有当直线b+c=0经过点A时，取得最大值，且为2；
经过点C时，取得最小值，且为0．
由题意可得0＜b+c＜2．

点评 本题考查二次函数的最值的求法，注意讨论对称轴与区间的关系，考查不等式的证明，注意运用线性规划的知识，求得最值，属于中档题．