
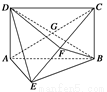
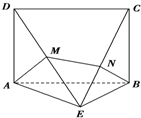
如图所示,矩形 中,
中,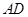 ⊥平面
⊥平面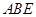 ,
,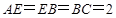 ,
, 为
为 上的点,且
上的点,且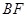 ⊥平面
⊥平面 .
.
(1)求证: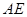 ⊥平面
⊥平面 ;
;
(2)求三棱锥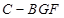 的体积.
的体积.
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
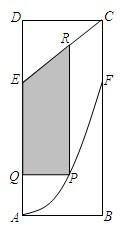 某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km,其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知AB=2km,BC=6km,AE=BF=4km,其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•深圳一模)如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE=
(2012•深圳一模)如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE=| 3 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省邯郸市高三上学期第二次模拟考试文科数学试卷(解析版) 题型:解答题
如图所示,矩形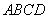 中,
中, ,
,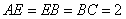 ,
, ,且
,且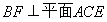 ,
, 交于点
交于点 .
.
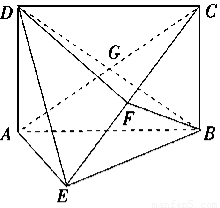
(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com