
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C: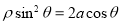 (a>0),过点P(-2,-4)的直线l的参数方程为
(a>0),过点P(-2,-4)的直线l的参数方程为 (t为参数),l与C分别交于M,N.
(t为参数),l与C分别交于M,N.
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
y2=2ax(a>0),x-y-2=0.a=1.
【解析】
试题分析:(1)曲线C的直角坐标方程为y2=2ax(a>0);
直线l的普通方程为x-y-2=0. 4分
(2)将直线l的参数方程与C的直角坐标方程联立,得
t2-2(4+a)  t+8(4+a)=0 (*)
t+8(4+a)=0 (*)
△=8a(4+a)>0.
设点M,N分别对应参数t1,t2,恰为上述方程的根.
则|PM|=|t1|,|PN|=|t2|,|MN|=|t1-t2|.
由题设得(t1-t2)2=|t1t2|,即(t1+t2)2-4t1t2=|t1t2|.
由(*)得t1+t2=2(4+a)  ,t1t2=8(4+a)>0,则有
,t1t2=8(4+a)>0,则有
(4+a)2-5(4+a)=0,得a=1,或a=-4.
因为a>0,所以a=1. 10分
考点:本题考查极坐标和参数方程
点评:(1)利用极坐标与普通方程的关系式,可得C为抛物线方程,消去参数t,可得直线l的方程;(2)由|PM|=|t1|,|MN|=|t1-t2|,|PN|=|t2|成等比数列,可转化为关于a的等量关系求解.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源:2014-2015学年山东省滕州市高一10月月考数学试卷(解析版) 题型:选择题
函数f(x)=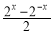 是( )
是( )
A.偶函数,在(0,+∞)是增函数
B.奇函数,在(0,+∞)是增函数
C.偶函数,在(0,+∞)是减函数
D.奇函数,在(0,+∞)是减函数
查看答案和解析>>
科目:高中数学 来源:2014-2015学年新疆师范大学附属中学高三12月月考文科数学试卷(解析版) 题型:解答题
对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此数据作出了频数与频率的统计表和频率分布直方图如下:
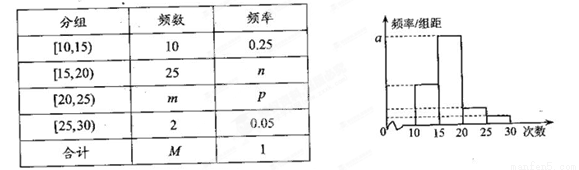
(1)求出表中M,p及图中a的值;
(2)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间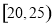 内的概率
内的概率
查看答案和解析>>
科目:高中数学 来源:2014-2015学年新疆师范大学附属中学高三12月月考文科数学试卷(解析版) 题型:选择题
己知函数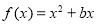 的图象在点
的图象在点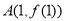 处的切线
处的切线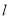 与直线3x- y+2=0平行,若数列
与直线3x- y+2=0平行,若数列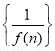 的前n项和为
的前n项和为 ,则
,则 的值为( )
的值为( )
A. B.
B. C.
C.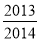 D.
D.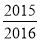
查看答案和解析>>
科目:高中数学 来源:2014-2015学年新疆师范大学附属中学高三12月月考理科数学试卷(解析版) 题型:解答题
已知函数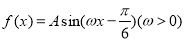 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是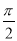 ,且满足,
,且满足, .
.
(1)求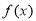 的单调递减区间;
的单调递减区间;
(2)在钝角△ABC中,a、b、c分别为角A、B、C的对边,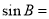
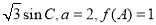 ,求△ABC的面积。
,求△ABC的面积。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省枣庄市高三第二次(1月)学情调查理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
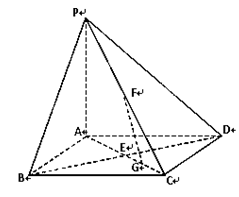
(1)求证:BD⊥FG;
(2)当二面角B—PC—D的大小为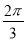 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com