练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(0)＝1，f(a－b)＝f(a)－b(2a－b＋1)，求f(x)．


    令a＝0，则f(－b)＝f(0)－b(－b＋1)＝1＋b(b－1)＝b2－b＋1

    再令－b＝x得：f(x)＝x2＋x＋1.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知下列四个命题：

    ①若tanθ＝2，则sin2θ＝；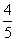

    ②函数f(x)＝lg(x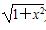＋是奇函数；

    ③“a>b”是“2a>2b”的充分不必要条件；

    ④在△ABC中，若sinAcosB＝sinC，则△ABC是直角三角形．

    其中所有真命题的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    求下列函数的定义域：

    y＝lg.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝若f(1)＋f(a)＝2，则a的值为(　　)

    A．1　　　　B．2　　　　C．4　　　　D．4或1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某地区预计2014年的前x个月内对某种商品的需求总量f(x)(万件)与月份x的近似关系式是f(x)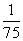＝x(x＋1)(19－x)，x∈N*,1≤x≤12，求：

    (1)2014年的第x月的需求量g(x)(万件)与月份x的函数关系式．

    (2)求第几个月需求量g(x)最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)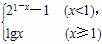＝若f(x0)>1，则x0的取值范围是(　　)

    A．(－∞，0)∪(10，＋∞)

    B．(－1，＋∞)

    C．(－∞，－2)∪(－1,10)

    D．(0,10)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝1－ (　　)

    A．在(－1，＋∞)内是增加的

    B．在(－1，＋∞)内是减少的

    C．在(1，＋∞)内是增加的

    D．在(1，＋∞)内是减少的

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a，b∈R，定义max{a，b}＝，函数f(x)＝max{|x＋1|，|x－2|}(x∈R)，则f(x)的最小值是______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝在定义域上为奇函数，则实数k＝________.

    查看答案和解析>>

    同步练习册答案