练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某地区预计2014年的前x个月内对某种商品的需求总量f(x)(万件)与月份x的近似关系式是f(x)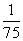＝x(x＋1)(19－x)，x∈N*,1≤x≤12，求：

    (1)2014年的第x月的需求量g(x)(万件)与月份x的函数关系式．

    (2)求第几个月需求量g(x)最大．


    　(1)第x月的需求量为g(x)＝f(x)－f(x－1)＝x(x＋1)(19－x)－(x－1)x(20－x)＝x(13－x)．

    (2)g(x)＝(－x2＋13x)＝－[42.25－(x－6.5)2]，因此当x＝6或7时g(x)最大．

    第6、7月需求量最大．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知条件p：函数g(x)＝logm(x－1)为减函数，条件q：关于x的二次方程x2－2x＋m＝0有解，则p是q的(　　)

    A．充分而不必要条件                                   B．必要而不充分条件

    C．充要条件                                                 D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义在R上的函数f(x)满足f(x＋1)＝2f(x)．若当0≤x≤1时，f(x)＝x(1－x)，则当－1≤x≤0时，f(x)＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝－的定义域为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝是(－∞，＋∞)上的增函数，那么a的取值范围是(　　)

    A．(1，＋∞)                                                B．(－∞，3)

    C．[，3)                                                   D．(1,3)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(0)＝1，f(a－b)＝f(a)－b(2a－b＋1)，求f(x)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


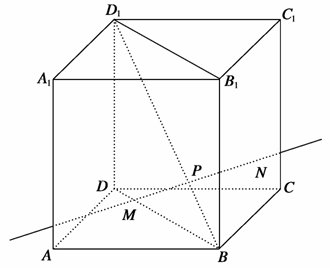
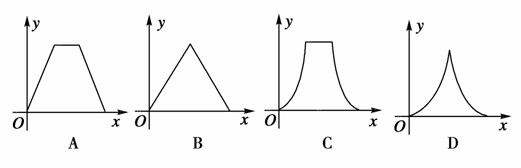
    如图，动点P在正方体ABCD－A1B1C1D1的对角线BD1上，过点P作垂直于平面BB1D1D的直线，与正方体表面相交于M、N.设BP＝x，MN＝y，则函数y＝f(x)的图象大致是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)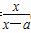＝ (x≠a)．

    (1)若a＝－2，试证f(x)在(－∞，－2)内单调递增；

    (2)若a>0且f(x)在(1，＋∞)内单调递减，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)为奇函数，且当x>0时，f(x)＝x2＋，则f(－1)＝(　　)

    A．－2                                                          B．0

    C．1                                                             D．2

    查看答案和解析>>

    同步练习册答案