
【题目】设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0;命题q:实数x满足|x﹣3|≤1.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
【答案】
(1)解:由x2﹣4ax+3a2<0得(x﹣3a)(x﹣a)<0
当a=1时,1<x<3,
即p为真时实数x的取值范围是1<x<3.
由|x﹣3|≤1,得﹣1≤x﹣3≤1,得2≤x≤4,
即q为真时实数x的取值范围是2≤x≤4,
若p∧q为真,则p真且q真,
所以实数x的取值范围是2≤x<3.
(2)解:由x2﹣4ax+3a2<0得(x﹣3a)(x﹣a)<0,p是q的充分不必要条件,
即pq,且qp,设A={x|p},B={x|q},则AB,
又A={x|p}={x|x≤a或x≥3a},B={x|q}={x|x>4 或 x<2},
则3a>4且a<2,其中a>0,
所以实数a的取值范围是 ![]() .
.
【解析】(1)若a=1,分别求出p,q成立的等价条件,利用且p∧q为真,求实数x的取值范围;(2)利用¬p是¬q的充分不必要条件,即q是p的充分不必要条件,求实数a的取值范围.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC-A′B′C′,底面是边长为1的正三角形,侧面为全等的矩形且高为8,求一点自A点出发沿着三棱柱的侧面绕行一周后到达A′点的最短路线长.

本题条件不变,求一点自A点出发沿着三棱柱的侧面绕行两周后到达A′点的最短路线长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=
∠ACD=90°,∠EAC=60°,AB=AC=AE.
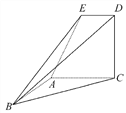
(1)在直线BC上是否存在一点P,使得DP∥平面EAB?请证明你的结论.
(2)求平面EBD与平面ABC所成的锐二面角θ的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P-ABCD的底面ABCD是正方形,E,F分别为AC和PB上的点,它的直观图,正视图,侧视图如图所示.
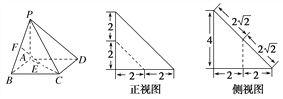
(1)求EF与平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,给出以下四个结论:
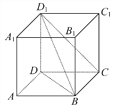
①D1C∥平面A1ABB1;②A1D1与平面BCD1相交;
③AD⊥平面D1DB;④平面BCD1⊥平面A1ABB1.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,BC=6,AC=3,D,E分别是AC,AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
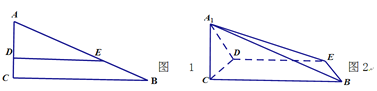
(1)求证:![]() 平面
平面![]() ;
;
(2)过点E作截面![]()
![]() 平面
平面![]() ,分别交CB于F,
,分别交CB于F,![]() 于H,求截面
于H,求截面![]() 的面积。
的面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,A(0,1),AB边上的高CD所在直线的方程为x+2y-4=0,AC边上的中线BE所在直线的方程为2x+y-3=0.
(1)求直线AB的方程;
(2)求直线BC的方程;
(3)求△BDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com