Question

【题目】函数 的部分图象如图所示，求：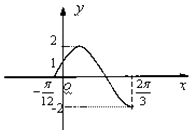
（1）f（x）的表达式．
（2）f（x）的单调增区间．
（3）f（x）的最小值以及取得最小值时的x集合．

Answer 1

【答案】
（1）解：根据函数 的部分图象，

可得A=2， = + ，求得ω=2，∴f（x）=2sin（2x+φ）．

再根据五点法作图可得2 +φ= ，∴φ= ，∴f（x）=2sin（2x+ ）

（2）解：令2kπ﹣ ≤2x+ ≤2kπ+ ，求得kπ﹣ ≤x≤kπ+ ，

可得函数的增区间为[kπ﹣ ，kπ+ ]，k∈Z

（3）解：令2x+ =2kπ﹣ ，求得x=kπ+﹣ ，可得当x=kπ+﹣ ，k∈Z 时，函数取得最小值为﹣2．

即f（x）的最小值为﹣2，取得最小值时的x集合为{x|x=kπ+﹣ ，k∈Z }

【解析】（1）由函数的最值求出A，由周期求出ω，由五点法作图求出φ的值，可得函数的解析式．（2）利用正弦函数的单调性，求得函数的增区间．（3）利用正弦函数的最值，求得f（x）的最小值以及取得最小值时的x集合．