练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数f（x）=2cos2x+ sin2x﹣1．
    （1）求f（x）的最大值及此时的x值
    （2）求f（x）的单调减区间
    （3）若x∈[﹣ ， ]时，求f（x）的值域．

    【答案】
    （1）解：f（x）=2cos2x+ sin2x﹣1=cos2x+ = ，

    当2x+ ，即 时，f（x）max=2


    （2）解：
    （3）解：由 ，得 ，

    ∴f（x）的单调减区间为[ ]，k∈Z；

    ，

    由 ，得 ，

    ∴ ，

    ∴﹣1≤f（x）≤2．

    则f（x）的值域为[﹣1，2]


    【解析】f（x）=2cos2x+ sin2x﹣1=cos2x+ （1）当2x+ ，即 时，f（x）取得最大值；（2）由 ，得 ，即可求出f（x）的单调减区间；（3）由 ，得 ，即可求出f（x）的值域．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面，底面是直角梯形，，，，是上的点．

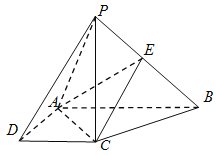
    （Ⅰ）求证：平面⊥平面；

    （Ⅱ）若是的中点，且二面角的余弦值为，求直线与平面所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次数学考试中，第22题和第23题为选做题，规定每位考生必须且只须在其中选做一题，现有甲、乙、丙、丁4名考生参加考试，其中甲、乙选做第22题的概率均为，丙、丁选做第22题的概率均为．

    (Ⅰ)求在甲选做第22题的条件下，恰有两名考生选做同一道题的概率；

    (Ⅱ)设这4名考生中选做第22题的学生个数为X，求X的概率分布及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数 的部分图象如图所示，求：
    （1）f（x）的表达式．
    （2）f（x）的单调增区间．
    （3）f（x）的最小值以及取得最小值时的x集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设在平面上有两个向量a=(cos 2α,sin 2α)(0≤α<π),b=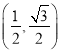,a与b不共线.

    (1)求证:向量a+b与a-b垂直;

    (2)当向量a+b与a-b的模相等时,求α的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，A、B、C的对边分别是a，b，c，且bcosB是acosC，ccosA的等差中项，则角B= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】东莞市某高级中学在今年4月份安装了一批空调，关于这批空调的使用年限（单位：年， ）和所支出的维护费用（单位：万元）厂家提供的统计资料如下：

    （1）请根据以上数据，用最小二乘法原理求出维护费用关于的线性回归方程；

    （2）若规定当维护费用超过13.1万元时，该批空调必须报废，试根据（1）的结论求该批空调使用年限的最大值.

    参考公式：最小二乘估计线性回归方程中系数计算公式：

    ，

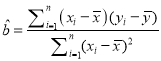    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，曲线的参数方程为为参数），以坐标原点为极点，以轴非负半轴为极轴建立极坐标系，直线的极坐标方程为.

    （1）求曲线的极坐标方程及直线的直角坐标方程；

    （2）设直线与曲线交于两点，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在菱形中，⊥平面，且四边形是平行四边形．

    （1）求证：；

    （2）当点在的什么位置时，使得∥平面，并加以证明．

    查看答案和解析>>

    同步练习册答案