
【题目】已知圆![]() 和圆
和圆![]() .
.
(1)判断圆![]() 和圆
和圆![]() 的位置关系;
的位置关系;
(2)过圆![]() 的圆心
的圆心![]() 作圆
作圆![]() 的切线
的切线![]() ,求切线
,求切线![]() 的方程;
的方程;
(3)过圆![]() 的圆心
的圆心![]() 作动直线
作动直线![]() 交圆
交圆![]() 于A,B两点.试问:在以AB为直径的所有圆中,是否存在这样的圆
于A,B两点.试问:在以AB为直径的所有圆中,是否存在这样的圆![]() ,使得圆
,使得圆![]() 经过点
经过点![]() ?若存在,求出圆
?若存在,求出圆![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)外离;
(2)![]() 或
或![]() ;
;
(3)存在圆![]() :
:![]() 或
或![]() ,使得圆
,使得圆![]() 经过点
经过点![]() 。
。
【解析】
试题分析:(1)求出两圆的圆心距,在比较其与![]() 的大小关系,从而确定两圆的位置关系;(2)由点
的大小关系,从而确定两圆的位置关系;(2)由点
斜式设出切线方程,然后用点线距离公式建立关于![]() 的方程;(2)斜率不存在时,易知圆
的方程;(2)斜率不存在时,易知圆![]() 也是满足题意的圆;斜率存在时,假设存在以
也是满足题意的圆;斜率存在时,假设存在以![]() 为直径的圆
为直径的圆![]() 经过点
经过点![]() ,则
,则![]() ,所以
,所以![]() ,则可得
,则可得![]() ,再把直线方程与圆
,再把直线方程与圆![]() 的方程联立可求
的方程联立可求![]() ,
,![]() ,代入上式可得关于
,代入上式可得关于![]() 的方程。
的方程。
(1)因为圆![]() 的圆心
的圆心![]()
![]() ,半径
,半径![]() ,圆
,圆![]() 的圆心
的圆心![]()
![]() ,径
,径![]() ,
,
所以圆![]() 和圆
和圆![]() 的圆心距
的圆心距![]() ,
,
所以圆![]() 与圆
与圆![]() 外离. 3分
外离. 3分
(2)设切线![]() 的方程为:
的方程为:![]() ,即
,即![]() ,
,
所以![]() 到
到![]() 的距离
的距离![]() ,解得
,解得![]() .
.
所以切线![]() 的方程为
的方程为![]() 或
或![]() . ....7分
. ....7分
(3)ⅰ)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 经过圆
经过圆![]() 的圆心
的圆心![]() ,此时直线
,此时直线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 即为圆
即为圆![]() 的直径,而点
的直径,而点![]() 在圆
在圆![]() 上,即圆
上,即圆![]() 也是满足题意的圆........8分
也是满足题意的圆........8分
ⅱ)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() ,由
,由 ,
,
消去![]() 整理,得
整理,得![]() ,
,
由△![]() ,得
,得![]() 或
或![]() .
.
设![]() ,则有
,则有 ① 9分
① 9分
由①得![]() , ②
, ②
![]() , ③
, ③
若存在以![]() 为直径的圆
为直径的圆![]() 经过点
经过点![]() ,则
,则![]() ,所以
,所以![]() ,
,
因此![]() ,即
,即![]() , 10分
, 10分
则![]() ,所以
,所以![]() ,
,![]() ,满足题意.
,满足题意.
此时以![]() 为直径的圆的方程为
为直径的圆的方程为![]() ,
,
即![]() ,亦即
,亦即![]() . 12分
. 12分
综上,在以AB为直径的所有圆中,存在圆![]() :
:![]() 或
或
![]() ,使得圆
,使得圆![]() 经过点
经过点![]() . 14分
. 14分


科目:高中数学 来源: 题型:
【题目】甲乙丙丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为 ![]() , 有以下结论:
, 有以下结论:
①当x>1时,甲在最前面;
②当x>1时,乙在最前面;
③当0<x<1时,丁在最前面,当x>1时,丁在最后面;
④丙不可能在最前面,也不可能最最后面;
⑤如果它们已知运动下去,最终在最前面的是甲.
其中,正确结论的序号为(把正确结论的序号都填上,多填或少填均不得分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞市某高级中学在今年4月份安装了一批空调,关于这批空调的使用年限![]() (单位:年,
(单位:年, ![]() )和所支出的维护费用
)和所支出的维护费用![]() (单位:万元)厂家提供的统计资料如下:
(单位:万元)厂家提供的统计资料如下:

(1)请根据以上数据,用最小二乘法原理求出维护费用![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若规定当维护费用![]() 超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
参考公式:最小二乘估计线性回归方程![]() 中系数计算公式:
中系数计算公式:
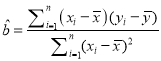 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆期间,高速公路堵车现象经常发生.某调查公司为了了解车速,在临川收费站从7座以下小型汽车中按进收费站的先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查,将他们在某段高速公路的车速![]() )分成六段
)分成六段![]() 后,得到如图的频率分布直方图.
后,得到如图的频率分布直方图.
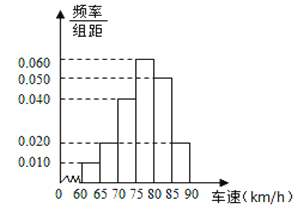
(1)求这40辆小型汽车车速的众数和中位数的估计值;
(2)若从这40辆车速在![]() 的小型汽车中任意抽取2辆,求抽出的2辆车车速都在
的小型汽车中任意抽取2辆,求抽出的2辆车车速都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,直线
轴非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程及直线
的极坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a等于 . 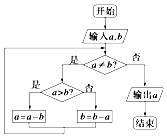
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A,B两名同学在5次数学考试中的成绩统计如下面的茎叶图所示,若A,B两人的平均成绩分别是xA , xB , 观察茎叶图,下列结论正确的是( ) 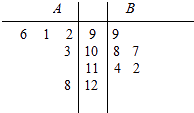
A.xA<xB , B比A成绩稳定
B.xA>xB , B比A成绩稳定
C.xA<xB , A比B成绩稳定
D.xA>xB , A比B成绩稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com