
ЁОЬтФПЁПЙњЧьЦкМфЃЌИпЫйЙЋТЗЖТГЕЯжЯѓОГЃЗЂЩњ.ФГЕїВщЙЋЫОЮЊСЫСЫНтГЕЫйЃЌдкСйДЈЪеЗбеОДг7зљвдЯТаЁаЭЦћГЕжаАДНјЪеЗбеОЕФЯШКѓЫГађЃЌУПМфИє50СООЭГщШЁвЛСОЕФГщбљЗНЗЈГщШЁ40СОЦћГЕНјааГщбљЕїВщЃЌНЋЫћУЧдкФГЖЮИпЫйЙЋТЗЕФГЕЫй![]() ЃЉЗжГЩСљЖЮ
ЃЉЗжГЩСљЖЮ![]() КѓЃЌЕУЕНШчЭМЕФЦЕТЪЗжВМжБЗНЭМ.
КѓЃЌЕУЕНШчЭМЕФЦЕТЪЗжВМжБЗНЭМ.
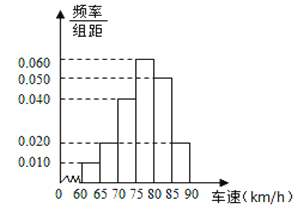
ЃЈ1ЃЉЧѓет40СОаЁаЭЦћГЕГЕЫйЕФжкЪ§КЭжаЮЛЪ§ЕФЙРМЦжЕЃЛ
ЃЈ2ЃЉШєДгет40СОГЕЫйдк![]() ЕФаЁаЭЦћГЕжаШЮвтГщШЁ2СОЃЌЧѓГщГіЕФ2СОГЕГЕЫйЖМдк
ЕФаЁаЭЦћГЕжаШЮвтГщШЁ2СОЃЌЧѓГщГіЕФ2СОГЕГЕЫйЖМдк![]() ЕФИХТЪЃЎ
ЕФИХТЪЃЎ
ЁОД№АИЁП(1) ![]() ,
, ![]() (2)
(2) ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃК
(1)РћгУЦЕТЪЗжВМжБЗНЭМПЩЙРМЦжкЪ§ЮЊ77.5ЃЌЪЙЕУжаЮЛЪ§ДІНЋЦЕТЪЗжВМжБЗНЭМЗжИюЮЊУцЛ§ЯрЕШЕФСНВПЗжЃЌОнДЫСаЗНГЬПЩЕУжаЮЛЪ§ЮЊ77.5ЃЛ
(2)РћгУЙХЕфИХаЭЙЋЪНПЩжЊЪТМўЕФИХТЪПеМфЙВга15жжВЛЭЌЕФНсЙћЃЌЦфжаТњзуЬтвтЕФНсЙћга6жжЃЌдђТњзуЬтвтЕФИХТЪжЕЮЊ![]() .
.
ЪдЬтНтЮіЃК
(1)жкЪ§ЕФЙРМЦжЕЮЊзюИпЕФОиаЮЕФжаЕуЃЌМДжкЪ§ЕФЙРМЦжЕЮЊ![]()
гЩЬтЭМПЩжЊЃЌжаЮЛЪ§гІИУдк![]() жЎМфЃЌЩшЮЊ
жЎМфЃЌЩшЮЊ![]() ЃЌ
ЃЌ
дђ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК ![]()
МДжаЮЛЪ§ЕФЙРМЦжЕЮЊ![]()
(2)ет![]() СОГЕжаЃЌГЕЫйдк
СОГЕжаЃЌГЕЫйдк![]() ЕФЙВга
ЕФЙВга![]() (СО)ЃЌ
(СО)ЃЌ
ЦфжаГЕЫйдк![]() ЕФга
ЕФга![]() (СО)ЃЌМЧЮЊ
(СО)ЃЌМЧЮЊ![]()
ГЕЫйдк![]() ЕФга
ЕФга![]() (СО)ЃЌМЧЮЊ
(СО)ЃЌМЧЮЊ![]() ДгГЕЫйдк
ДгГЕЫйдк![]() ЕФет
ЕФет![]() СОЦћГЕжаШЮвтГщШЁ
СОЦћГЕжаШЮвтГщШЁ![]() СОЕФПЩФмНсЙћга
СОЕФПЩФмНсЙћга![]() жжВЛЭЌЕФНсЙћЃЌ
жжВЛЭЌЕФНсЙћЃЌ
ЦфжаГщГіЕФ![]() СОГЕГЕЫйЖМдк
СОГЕГЕЫйЖМдк![]() ЕФНсЙћга
ЕФНсЙћга![]() жж
жж
вђЮЊГщЕНУПжжНсЙћЖМЪЧЕШПЩФмЕФЃЌЫљвдДгет![]() СОГЕЫйдк
СОГЕЫйдк![]() ЕФЦћГЕжаШЮвтГщШЁ
ЕФЦћГЕжаШЮвтГщШЁ![]() СОЃЌ
СОЃЌ
ГщГіЕФ![]() СОГЕГЕЫйЖМдк
СОГЕГЕЫйЖМдк![]() ЕФИХТЪЮЊ
ЕФИХТЪЮЊ![]()


 бЇСЗПьГЕЕРПьРжМйЦкКЎМйзївЕЯЕСаД№АИ
бЇСЗПьГЕЕРПьРжМйЦкКЎМйзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЦНУцФквЛЖЏЕу![]() гыСНЖЈЕу
гыСНЖЈЕу![]() КЭ
КЭ![]() СЌЯпЕФаБТЪжЎЛ§ЕШгк
СЌЯпЕФаБТЪжЎЛ§ЕШгк![]() .
.
ЃЈЂёЃЉЧѓЖЏЕу![]() ЕФЙьМЃ
ЕФЙьМЃ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈЂђЃЉЩшжБЯп![]() ЃК
ЃК ![]() ЃЈ
ЃЈ![]() ЃЉгыЙьМЃ
ЃЉгыЙьМЃ![]() НЛгк
НЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЯпЖЮ
СНЕуЃЌЯпЖЮ![]() ЕФДЙжБЦНЗжЯпНЛ
ЕФДЙжБЦНЗжЯпНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЕБ
ЃЌЕБ![]() БфЛЏЪБЃЌЧѓ
БфЛЏЪБЃЌЧѓ![]() УцЛ§ЕФзюДѓжЕ.
УцЛ§ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГБЃЯеЙЋЫОеыЖдЦѓвЕжАЙЄЭЦГівЛПювтЭтЯеВњЦЗЃЌУПФъУПШЫжЛвЊНЛЩйСПБЃЗбЃЌЗЂЩњвтЭтКѓПЩвЛДЮадЛёХт50ЭђдЊ.БЃЯеЙЋЫОАбжАЙЄДгЪТЕФЫљгаИкЮЛЙВЗжЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§РрЙЄжжЃЌИљОнРњЪЗЪ§ОнЭГМЦГіШ§РрЙЄжжЕФУПХтИЖЦЕТЪШчЯТБэЃЈВЂвдДЫЙРМЦХтИЖИХТЪЃЉ.
Ш§РрЙЄжжЃЌИљОнРњЪЗЪ§ОнЭГМЦГіШ§РрЙЄжжЕФУПХтИЖЦЕТЪШчЯТБэЃЈВЂвдДЫЙРМЦХтИЖИХТЪЃЉ.


ЃЈЂёЃЉИљОнЙцЖЈЃЌИУВњЦЗИїЙЄжжБЃЕЅЕФЦкЭћРћШѓЖМВЛЕУГЌЙ§БЃЗбЕФ20%ЃЌЪдЗжБ№ШЗЖЈИїРрЙЄжжУПеХБЃЕЅБЃЗбЕФЩЯЯоЃЛ
ЃЈЂђЃЉФГЦѓвЕЙВгажАЙЄ20000ШЫЃЌДгЪТШ§РрЙЄжжЕФШЫЪ§ЗжВМБШР§ШчЭМЃЌРЯАхзМБИЮЊШЋЬхжАЙЄУПШЫЙКТђвЛЗнДЫжжБЃЯеЃЌВЂвдЃЈЂёЃЉжаМЦЫуЕФИїРрБЃЯеЩЯЯоЙКТђЃЌЪдЙРМЦБЃЯеЙЋЫОдкетзкНЛвзжаЕФЦкЭћРћШѓ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]()
ЃЈ1ЃЉШєКЏЪ§![]() гаСуЕуЃЌЧѓЪЕЪ§
гаСуЕуЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉжЄУїЃКЕБ![]() ЪБЃЌ
ЪБЃЌ ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВ![]() КЭдВ
КЭдВ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉХаЖЯдВ![]() КЭдВ
КЭдВ![]() ЕФЮЛжУЙиЯЕЃЛ
ЕФЮЛжУЙиЯЕЃЛ
ЃЈ2ЃЉЙ§дВ![]() ЕФдВаФ
ЕФдВаФ![]() зїдВ
зїдВ![]() ЕФЧаЯп
ЕФЧаЯп![]() ЃЌЧѓЧаЯп
ЃЌЧѓЧаЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ3ЃЉЙ§дВ![]() ЕФдВаФ
ЕФдВаФ![]() зїЖЏжБЯп
зїЖЏжБЯп![]() НЛдВ
НЛдВ![]() гкAЃЌBСНЕуЃЎЪдЮЪЃКдквдABЮЊжБОЖЕФЫљгадВжаЃЌЪЧЗёДцдкетбљЕФдВ
гкAЃЌBСНЕуЃЎЪдЮЪЃКдквдABЮЊжБОЖЕФЫљгадВжаЃЌЪЧЗёДцдкетбљЕФдВ![]() ЃЌЪЙЕУдВ
ЃЌЪЙЕУдВ![]() ОЙ§Еу
ОЙ§Еу![]() ЃПШєДцдкЃЌЧѓГідВ
ЃПШєДцдкЃЌЧѓГідВ![]() ЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФЗНГЬЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкКЏЪ§fЃЈxЃЉ=sinЃЈ2x+ ![]() ЃЉЃЌЯТСаУќЬтЃК ЂйКЏЪ§ЭМЯѓЙигкжБЯпx=Љ
ЃЉЃЌЯТСаУќЬтЃК ЂйКЏЪ§ЭМЯѓЙигкжБЯпx=Љ ![]() ЖдГЦЃЛ
ЖдГЦЃЛ
ЂкКЏЪ§ЭМЯѓЙигкЕуЃЈ ![]() ЃЌ0ЃЉЖдГЦЃЛ
ЃЌ0ЃЉЖдГЦЃЛ
ЂлКЏЪ§ЭМЯѓПЩПДзїЪЧАбy=sin2xЕФЭМЯѓЯђзѓЦНвЦИі ![]() ЕЅЮЛЖјЕУЕНЃЛ
ЕЅЮЛЖјЕУЕНЃЛ
ЂмКЏЪ§ЭМЯѓПЩПДзїЪЧАбy=sinЃЈx+ ![]() ЃЉЕФЭМЯѓЩЯЫљгаЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ
ЃЉЕФЭМЯѓЩЯЫљгаЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ ![]() БЖЃЈзнзјБъВЛБфЃЉЖјЕУЕНЃЛЦфжае§ШЗЕФУќЬтЪЧ ЃЎ
БЖЃЈзнзјБъВЛБфЃЉЖјЕУЕНЃЛЦфжае§ШЗЕФУќЬтЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДКНкРДСйЃЌгаХЉУёЙЄажЕм![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЫФШЫИїздЭЈЙ§ЛЅСЊЭјЖЉЙКЛиМвЙ§ФъЕФЛ№ГЕЦБЃЌШєЖЉЦБГЩЙІМДПЩЛёЕУЛ№ГЕЦБЃЌМДЫћУЧЛёЕУЛ№ГЕЦБгыЗёЛЅВЛгАЯь.Шє
ЫФШЫИїздЭЈЙ§ЛЅСЊЭјЖЉЙКЛиМвЙ§ФъЕФЛ№ГЕЦБЃЌШєЖЉЦБГЩЙІМДПЩЛёЕУЛ№ГЕЦБЃЌМДЫћУЧЛёЕУЛ№ГЕЦБгыЗёЛЅВЛгАЯь.Шє![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЛёЕУЛ№ГЕЦБЕФИХТЪЗжБ№ЪЧ
ЛёЕУЛ№ГЕЦБЕФИХТЪЗжБ№ЪЧ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌгж
ЃЌгж![]() ГЩЕШБШЪ§СаЃЌЧв
ГЩЕШБШЪ§СаЃЌЧв![]() ЁЂ
ЁЂ![]() СНШЫЧЁКУгавЛШЫЛёЕУЛ№ГЕЦБЕФИХТЪЪЧ
СНШЫЧЁКУгавЛШЫЛёЕУЛ№ГЕЦБЕФИХТЪЪЧ![]() .
.
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШє![]() ЁЂ
ЁЂ![]() ЪЧвЛМвШЫЧвСНШЫЖМЛёЕУЛ№ГЕЦБВХвЛЦ№ЛиМвЃЌЗёдђСНШЫЖМВЛЛиМв.Щш
ЪЧвЛМвШЫЧвСНШЫЖМЛёЕУЛ№ГЕЦБВХвЛЦ№ЛиМвЃЌЗёдђСНШЫЖМВЛЛиМв.Щш![]() БэЪО
БэЪО![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ФмЙЛЛиМвЙ§ФъЕФШЫЪ§ЃЌЧѓ
ФмЙЛЛиМвЙ§ФъЕФШЫЪ§ЃЌЧѓ![]() ЕФЗжВМСаКЭЦкЭћ
ЕФЗжВМСаКЭЦкЭћ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТБэЬсЙЉСЫФГГЇНкФмНЕКФММЪѕИФНјКѓЩњВњМзВњЦЗЙ§ГЬжаМЧТМЕФВњСПxЃЈЖжЃЉгыЯргІЕФЩњВњФмКФyЃЈЖжБъзМУКЃЉЕФМИзщЖдееЪ§ОнЃЎ
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
ЃЈ1ЃЉЧыИљОнЩЯБэЬсЙЉЕФЪ§ОнЃЌгУзюаЁЖўГЫЗЈЧѓГіyЙигкxЕФЛиЙщЗНГЬ ![]() =
= ![]() x+
x+ ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉвбжЊИУГЇММИФЧА100ЖжМзВњЦЗЕФЩњВњФмКФЮЊ90ЖжБъзМУКЃЎЪдИљОнЃЈ1ЃЉЧѓГіЕФЛиЙщЗНГЬЃЌдЄВтЩњВњ100ЖжМзВњЦЗЕФЩњВњФмКФБШММИФЧАНЕЕЭЖрЩйЖжБъзМУКЃП ЃЈВЮПМЪ§жЕЃК3ЁС2.5+4ЁС3+5ЁС4+6ЁС4.5=66.5ЃЉМЦЫуЛиЙщЯЕЪ§ ![]() ЃЌ
ЃЌ ![]() ЃЎЙЋЪНЮЊ
ЃЎЙЋЪНЮЊ 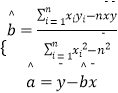 ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЮЊСЫПМКЫМзЃЌввСНВПУХЕФЙЄзїЧщПіЃЌЫцЛњЗУЮЪСЫ50ЮЛЪаУёЃЌИљОнет50ЮЛЪаУёЖдетСНВПУХЕФЦРЗжЃЈЦРЗждНИпБэУїЪаУёЕФЦРМлдНИпЃЉЃЌЛцжЦОЅвЖЭМШчЯТЃК

ЃЈ1ЃЉЗжБ№ЙРМЦИУЪаЕФЪаУёЖдМзЃЌввСНВПУХЦРЗжЕФжаЮЛЪ§ЃЛ
ЃЈ2ЃЉЗжБ№ЙРМЦИУЪаЕФЪаУёЖдМзЃЌввСНВПУХЕФЦРЗжИпгк90ЕФИХТЪЃЛ
ЃЈ3ЃЉИљОнОЅвЖЭМЗжЮіИУЪаЕФЪаУёЖдМзЃЌввСНВПУХЕФЦРМлЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com