
【题目】已知函数![]()
(1)若函数![]() 有零点,求实数
有零点,求实数![]() 的取值范围;
的取值范围;
(2)证明:当![]() 时,
时, ![]()
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】试题分析:(I)对函数求导,可得函数单调性,并求得函数的最小值,若函数有零点,函数最小值小于零且在定义域范围有函数值大于零,解不等式可得![]() 的范围;(Ⅱ)将
的范围;(Ⅱ)将![]() 代入不等式化简为
代入不等式化简为![]() ,可构造函数
,可构造函数![]()
![]() 利用导数判断单调性可知在
利用导数判断单调性可知在![]() 条件下
条件下![]() 最小值为
最小值为![]() ,
, ![]() 最大值为
最大值为![]() .可证命题.
.可证命题.
试题解析:
(Ⅰ)法1: 函数![]() 的定义域为
的定义域为![]() .
.
由![]() , 得
, 得![]() .
.
因为![]() ,则
,则![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() .
.
所以函数![]() 在
在![]() 上单调递减, 在
上单调递减, 在![]() 上单调递增.
上单调递增.
当![]() 时,
时, ![]() .
.
当![]() , 即
, 即![]() 时, 又
时, 又![]() , 则函数
, 则函数![]() 有零点.
有零点.
所以实数![]() 的取值范围为
的取值范围为![]() .
.
法2:函数![]() 的定义域为
的定义域为![]() .
.
由![]() , 得
, 得![]() .
.
令![]() ,则
,则![]() .
.
当![]() 时,
时, ![]() ; 当
; 当![]() 时,
时, ![]() .
.
所以函数![]() 在
在![]() 上单调递增, 在
上单调递增, 在![]() 上单调递减.
上单调递减.
故![]() 时, 函数
时, 函数![]() 取得最大值
取得最大值![]() .
.
因而函数![]() 有零点, 则
有零点, 则![]() .
.
所以实数![]() 的取值范围为
的取值范围为![]() .
.
(Ⅱ) 要证明当![]() 时,
时, ![]() ,
,
即证明当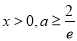 时,
时, ![]() , 即
, 即![]() .
.
令![]() , 则
, 则![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以函数![]() 在
在![]() 上单调递减, 在
上单调递减, 在![]() 上单调递增.
上单调递增.
当![]() 时,
时, ![]() .
.
于是,当![]() 时,
时, ![]() ①
①
令![]() , 则
, 则![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以函数![]() 在
在![]() 上单调递增, 在
上单调递增, 在![]() 上单调递减.
上单调递减.
当![]() 时,
时, ![]() .
.
于是 当![]() 时,
时, ![]() ②
②
显然, 不等式①、②中的等号不能同时成立.
故当![]() 时,
时, ![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】(2016·雅安高一检测)已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)-f(x+2),
(1)求g(x)的解析式及定义域;
(2)求函数g(x)的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时, ![]() .
.

(1)求函数![]() 的解析式;
的解析式;
(2)现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,请补全完整函数
轴左侧的图象,如图所示,请补全完整函数![]() 的图象;
的图象;
(3)根据(2)中画出的函数图像,直接写出函数![]() 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
, ![]() ,过
,过![]() 与坐标轴不垂直的直线
与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 为
为![]() ,
, ![]() 的中点.
的中点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,且
,且![]() ,求直线
,求直线![]() 所在的直线方程.
所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是数学家伯努瓦·曼德尔布罗在![]() 世纪
世纪![]() 年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图所示的分形规律可得如图乙所示的一个树形图:
年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图所示的分形规律可得如图乙所示的一个树形图:
若记图乙中第![]() 行白圈的个数为
行白圈的个数为![]() ,则
,则![]() __________.
__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某小区准备将闲置的一直角三角形(其中∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.
a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.

(1)若θ=![]() 时,绿地“最美”,求最美绿地的面积;
时,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民的行走,设计时要求将AN,A′N的值设计最短,求此时绿地公共走道的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com