练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知，．

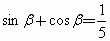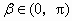    (1)求tanβ的值；

    (2)你能根据所给的条件，自己构造出一些求值问题吗？

    答案：略
    解析：

    (1)由可得．

    解得　或(由，舍去)．

    所以　．

    于是　．

    (2)根据所给条件，可求出仅由表示的三角函数式的值．例如，，等等．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    设a、b是方程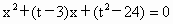的两个实根，并已知函数．

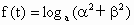    (1)求函数f(t)的解析式与定义域；

    (2)讨论函数f(t)的单调性；

    (3)当a=2时，求f(t)在定义域上的最大值与最小值．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江西南昌10所省高三第二次模拟冲刺理科数学试卷（二）（解析版） 题型：解答题

    已知向量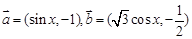,函数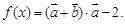

    (1)求函数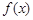的最小正周期T及单调减区间;

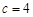    (2)已知a，b，c分别为ABC内角A，B，C的对边，其中A为锐角，,,且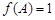.求A，b的长和ABC的面积.

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年福建省福州市八县（市）协作校高三上学期期中联考理科数学卷 题型：解答题

    （本题14分）已知函数,。

    (1)当t=8时，求函数的单调区间；

    （2）求证：当时，对任意正实数都成立；

    （3）若存在正实数，使得对任意的正实数都成立，请直接写出满足这样条件的一个的值（不必给出求解过程）

     

    查看答案和解析>>

    科目：高中数学 来源：2012届湖北省高三12月月考理科数学试卷 题型：解答题

    已知函数=，.

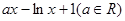    (1)求函数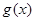在区间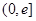上的值域T；

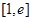    (2)是否存在实数，对任意给定的集合T中的元素t，在区间上总存在两个不同的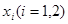，使得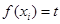成立.若存在，求出的取值范围；若不存在，请说明理由；

    (3

     

      

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在直角坐标系xOy上取两个定点A1(－2,0)，A2(2,0)，再取两个动点N1(0，m)，N2(0，n)，且mn＝3.

    (1)求直线A1N1与A2N2交点的轨迹M的方程；

    (2)已知点A(1，t)(t＞0)是轨迹M上的定点，E，F是轨迹M上的两个动点，如果直线AE的斜率kAE与直线AF的斜率kAF满足kAE＋kAF＝0，试探究直线EF的斜率是否是定值？若是定值，求出这个定值，若不是，说明理由．

    查看答案和解析>>

    同步练习册答案