
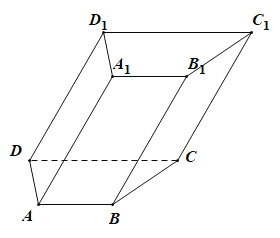
【题目】如图,四棱柱![]() ,底面
,底面![]() 为等腰梯形,
为等腰梯形,![]() ;
;![]() ,侧面
,侧面![]() 底面
底面![]() .
.
(1)在侧面![]() 中能否作一条直线使其与
中能否作一条直线使其与![]() 平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由;
平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由;
(2)求四面体![]() 的体积.
的体积.
【答案】(1)不能,理由见解析;(2)![]() .
.
【解析】
(1)假设在侧面![]() 中存在线段
中存在线段![]() 满足条件,得到
满足条件,得到![]() 平面
平面![]() ,利用线面平行的性质定理,证得
,利用线面平行的性质定理,证得![]() ,得出矛盾,即可求解;
,得出矛盾,即可求解;
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,分别证得
,分别证得![]() 平面
平面![]() 和
和![]() 平面
平面![]() ,进而证得
,进而证得![]() 平面
平面![]() ,得到四棱柱的高为
,得到四棱柱的高为![]() ,结合体积公式,即可求解.
,结合体积公式,即可求解.
(1)不能做出这样的直线段,
理由如下:假设在侧面![]() 中存在线段
中存在线段![]() 满足条件,
满足条件,
则由于![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() ,
,
这与等腰梯形![]() 中,
中,![]() 矛盾,所以假设错误,
矛盾,所以假设错误,
即侧面![]() 中不存在满足条件的直线段.
中不存在满足条件的直线段.
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,
因为![]() ,
,![]() ,可得
,可得![]() 为等边三角形,
为等边三角形,
所以![]() ,
,![]() .
.
因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
同理可证![]() 平面
平面![]() .
.
又因为![]() ,
,![]() ,
,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
因为平面![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
可得![]() 平面
平面![]() ,即四棱柱的高为
,即四棱柱的高为![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以![]()
![]()
![]() .
.


科目:高中数学 来源: 题型:
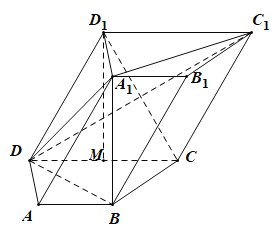
【题目】在日常生活中,石子是我们经常见到的材料,比如在各种建筑工地或者建材市场上常常能看到堆积如山的石子,它的主要成分是碳酸钙.某雕刻师计划在底面边长为2m、高为4m的正四棱柱形的石料![]() 中,雕出一个四棱锥
中,雕出一个四棱锥![]() 和球M的组合体,其中O为正四棱柱的中心,当球的半径r取最大值时,该雕刻师需去除的石料约重___________kg.(最后结果保留整数,其中
和球M的组合体,其中O为正四棱柱的中心,当球的半径r取最大值时,该雕刻师需去除的石料约重___________kg.(最后结果保留整数,其中![]() ,石料的密度
,石料的密度![]() ,质量
,质量![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
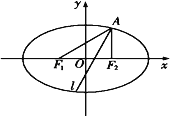
【题目】如图所示,已知椭圆E经过点![]() ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点![]() ,
,![]() 在x轴上,离心率e
在x轴上,离心率e![]() .直线l是
.直线l是![]() 的平分线,则椭圆E的方程是_____,l所在的直线方程是_____.
的平分线,则椭圆E的方程是_____,l所在的直线方程是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 只有一个公共点,点
只有一个公共点,点![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(1)求抛物线![]() 的方程;
的方程;
(2)①若![]() ,求证:直线
,求证:直线![]() 过定点;
过定点;
②若![]() 是抛物线
是抛物线![]() 上与原点不重合的定点,且
上与原点不重合的定点,且![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校高三大理班周三上午四节、下午三节有六门科目可供安排,其中语文和数学各自都必须上两节而且两节连上,而英语、物理、化学、生物最多上一节,则不同的功课安排有________种情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数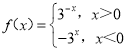 ,若
,若![]() ,b=f(log24.2),c=f(20.7),则a,b,c的大小关系为( )
,b=f(log24.2),c=f(20.7),则a,b,c的大小关系为( )
A.a<b<cB.b<a<cC.c<a<bD.c<b<a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将曲线方程![]() ,先向左平移2个单位,再向上平移2个单位,得到曲线C.
,先向左平移2个单位,再向上平移2个单位,得到曲线C.
(1)点M(x,y)为曲线C上任意一点,写出曲线C的参数方程,并求出![]() 的最大值;
的最大值;
(2)设直线l的参数方程为![]() ,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
,(t为参数),又直线l与曲线C的交点为E,F,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段EF的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
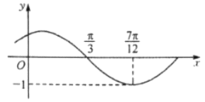
【题目】函数![]() 的图象如图所示,先将函数
的图象如图所示,先将函数![]() 图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移
图象上所有点的横坐标变为原来的6倍,纵坐标不变,再将所得函数的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,下列结论正确的是( )
的图象,下列结论正确的是( )
A.函数![]() 是奇函数B.函数
是奇函数B.函数![]() 在区间
在区间![]() 上是增函数
上是增函数
C.函数![]() 图象关于
图象关于![]() 对称D.函数
对称D.函数![]() 图象关于直线
图象关于直线![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD为矩形,点A、E、B、F共面,![]() 和
和![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() 若平面
若平面![]() ⊥平面
⊥平面![]()
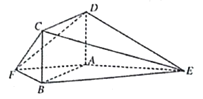
(Ⅰ)证明:平面![]() 平面ADF
平面ADF
(Ⅱ)问在线段EC上是否存在一点G,使得BG∥平面![]() 若存在,求出此时三棱锥G一ABE与三棱锥
若存在,求出此时三棱锥G一ABE与三棱锥![]() 的体积之比,若不存在,请说明理由.
的体积之比,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com