
分析 (1)f(x)中的x换上1便可求出f(1),从而可求出a=-2;
(2)根据减函数的定义,在区间(-1,1)上设任意的x1<x2,然后作差,通分,提取公因式x2-x1,从而证明f(x1)>f(x2),这样便可得到f(x)在(-1,1)上单调递减;
(3)根据f(x)解析式,显然可得到f(-x)=-f(x),从而由原不等式可得到f(t-1)<f(-t),这样根据f(x)的定义域和单调性便可得到关于t的不等式组,解不等式组即可得出原不等式的解集.
解答 解:(1)f(1)=$\frac{a}{2}=-1$;
∴a=-2;
(2)证明:$f(x)=-\frac{2x}{{1+{x^2}}}$,设x1,x2∈(-1,1),且x1<x2,则:
$f({x}_{1})-f({x}_{2})=\frac{2{x}_{2}}{1+{{x}_{2}}^{2}}-\frac{2{x}_{1}}{1+{{x}_{1}}^{2}}$=$\frac{2({x}_{2}-{x}_{1})(1-{x}_{1}{x}_{2})}{(1+{{x}_{2}}^{2})(1+{{x}_{1}}^{2})}$;
∵-1<x1<x2<1;
∴x2-x1>0,-1<x1x2<1,1-x1x2>0;
∴$\frac{2({x}_{2}-{x}_{1})(1-{x}_{1}{x}_{2})}{(1+{{x}_{2}}^{2})(1+{{x}_{1}}^{2})}>0$;
∴f(x1)>f(x2);
∴f(x)在区间(-1,1)上单调递减;
(3)显然f(-x)=-f(x);
∴由f(t-1)+f(t)<0得:f(t-1)<f(-t);
由(2)知f(x)在定义域[-1,1]上单调递减;
∴$\left\{\begin{array}{l}{-1≤t-1≤1}\\{-1≤-t≤1}\\{t-1>-t}\end{array}\right.$;
解得$\frac{1}{2}<t≤1$;
∴原不等式的解集为$(\frac{1}{2},1]$.
点评 考查已知函数求值,减函数的定义,以及根据减函数的定义证明一个函数为减函数的方法和过程,作差的方法比较f(x1),f(x2),作差后是分式的一般要通分,一般要提取公因式x1-x2,或x2-x1,奇函数的定义,根据单调性的定义解不等式的方法.


科目:高中数学 来源: 题型:选择题
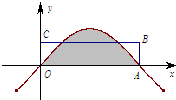 点A是函数f(x)=sinx的图象与x轴的一个交点(如图所示),若图中阴影部分的面积等于矩形OABC的面积,那么边AB的长等于( )
点A是函数f(x)=sinx的图象与x轴的一个交点(如图所示),若图中阴影部分的面积等于矩形OABC的面积,那么边AB的长等于( )| A. | $\frac{1}{π}$ | B. | $\frac{2}{π}$ | C. | $\frac{3}{π}$ | D. | $\frac{4}{π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 96 | B. | 108 | C. | 145 | D. | 160 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (310-1)2 | B. | $\frac{{{9^{10}}-1}}{2}$ | C. | 910-1 | D. | $\frac{{{3^{10}}-1}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
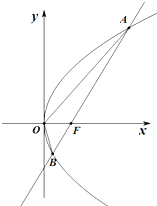 已知抛物线C:y2=2px(p>0)的焦点为F(1,0),过F且斜率为1的直线l交抛物线C于A(x1,y1),B(x2,y2)两点.
已知抛物线C:y2=2px(p>0)的焦点为F(1,0),过F且斜率为1的直线l交抛物线C于A(x1,y1),B(x2,y2)两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 总计 | |
| 优秀 | 15 | 15 | 30 |
| 非优秀 | |||
| 总计 | 45 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com