
【题目】已知圆![]() ,某抛物线的顶点为原点
,某抛物线的顶点为原点![]() ,焦点为圆心
,焦点为圆心![]() ,经过点
,经过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,交此抛物线于
两点,交此抛物线于![]() ,
, ![]() 两点,其中
两点,其中![]() ,
, ![]() 在第一象限,
在第一象限, ![]() ,
, ![]() 在第二象限.
在第二象限.
(1)求该抛物线的方程;
(2)是否存在直线![]() ,使
,使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在点
在点![]() 处切线方程为y=3x+b,求a,b的值;
处切线方程为y=3x+b,求a,b的值;
(Ⅱ)当a>0时,求函数![]() 在[1,2]上的最小值;
在[1,2]上的最小值;
(Ⅲ)设![]() ,若对任意
,若对任意![]() ,均存在
,均存在![]() ,使得
,使得![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60)…[90,100]后,画出如下部分频率分布直方图.观察图形的信息,回答下列问题: (Ⅰ) 求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 设学生甲、乙的成绩属于区间[40,50),现从成绩属于该区间的学生中任选两人,求甲、乙中至少有一人被选的概率.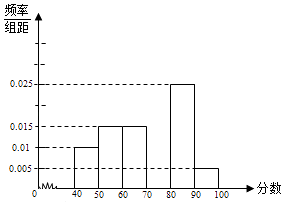
查看答案和解析>>
科目:高中数学 来源: 题型:
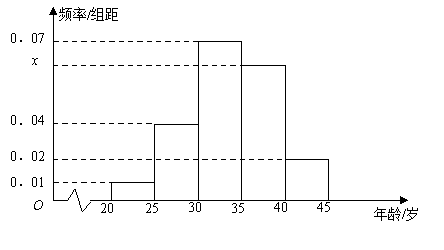
【题目】为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者. 从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是: ![]() .
.
(Ⅰ)求图中![]() 的值,并根据频率分布直方图估计这500名志愿者中年龄在
的值,并根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数;
岁的人数;
(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人. 记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() (其中p2+q2≠0),且存在公差不为0的无穷等差数列{an},使得函数在其定义域内还可以表示为f(x)=1+a1x+a2x+a2x2+…+anxn+…
(其中p2+q2≠0),且存在公差不为0的无穷等差数列{an},使得函数在其定义域内还可以表示为f(x)=1+a1x+a2x+a2x2+…+anxn+…
(1)求a1 , a2的值(用p,q表示);
(2)求{an}的通项公式;
(3)当n∈N*且n≥2时,比较(an﹣1)an与(an) ![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的是( )
A.各个面都是三角形的几何体是三棱锥
B.一平面截一棱锥得到一个棱锥和一个棱台
C.棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是正六棱锥
D.圆锥的顶点与底面圆周上的任意一点的连线都是母线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com