
分析 (1)先求出直线AC的斜率,从而得到AC边上的高BD的斜率,由此利用点斜式方程能求出BD所在的直线方程.
(2)先求出线段BC的中点和直线BC的斜率,从而得到BC边的垂直平分线EF的斜率,由此利用点斜式方程能求出BC边的垂直平分线EF所在直线方程.
解答 解:(1)∵△ABC的三个顶点A(3,-6),B(-5,0),C(-1,6),
∴直线AC的斜率kAC=$\frac{6+6}{-1-3}$=-3,
∴AC边上的高BD的斜率kBD=-$\frac{1}{{k}_{AC}}$=$\frac{1}{3}$,
∴BD所在的直线方程为:y=$\frac{1}{3}$(x+5),
整理,得x-3y+5=0.
(2)∵B(-5,0),C(-1,6),
∴线段BC的中点为(-3,3),直线BC的斜率$k=\frac{6-0}{-1+5}$=$\frac{3}{2}$,
∴BC边的垂直平分线EF的斜率kEF=-$\frac{1}{k}$=-$\frac{2}{3}$,
∴BC边的垂直平分线EF所在直线方程为:y-3=-$\frac{2}{3}$(x+3),
整理,得2x+3y-3=0.
点评 本题考查直线方程的求法,是基础题,解题时要认真审题,注意直线斜率公式、点斜式方程、中点坐标公式、直线垂直的性质的合理运用.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
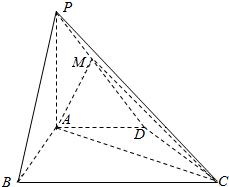 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com