
 已知函数f(x)=x|x-2|,
已知函数f(x)=x|x-2|,分析 (1)化绝对值函数为分段函数,画图即可,并由图得到单调区间,
(2)需要分类讨论,根据a的范围求出最值,
(3)由图象直接得到m,n的范围.
解答 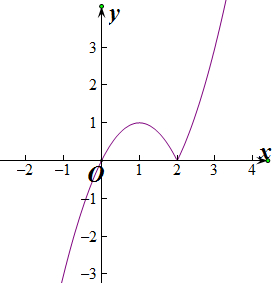 解:(1)f(x)=x|x-2|=$\left\{\begin{array}{l}{{x}^{2}-2x,x≥2}\\{-{x}^{2}+2x,x<2}\end{array}\right.$,
解:(1)f(x)=x|x-2|=$\left\{\begin{array}{l}{{x}^{2}-2x,x≥2}\\{-{x}^{2}+2x,x<2}\end{array}\right.$,
由图象可知,函数y=f(x)的单调递增区间为(-∞,1)∪(2,+∞);
(2)f(x)在闭区间[0,a]上最大值,
当a≤1,f(x)max=f(a)=-a2+2a,
令x2-2x=1,解得x=1+$\sqrt{2}$,
当1<a≤1+$\sqrt{2}$时,f(x)max=f(1)=1,
当a>1+$\sqrt{2}$时,f(x)max=f(a)=a2-2a;
(3)由图象可知,函数f(x)在开区间(m,n)上既有最大值又有最小值,
则0<m<1,2<n<1+$\sqrt{2}$,
点评 本题考查了函数图象的识别和画法,以及分类讨论的思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | $\frac{{8\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10岁时身高一定是145.83cm | B. | 每长大一岁身高就增高73.93cm | ||
| C. | 每长大一岁身高就增高81.12cm | D. | 10岁时身高在145.83cm左右 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sina)>f(cosb) | B. | f(sina)<f(cosb) | C. | f(cosa)<f(cosb) | D. | f(cosa)>f(cosb) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
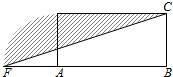 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )| A. | (4π+8)cm2 | B. | (4π+16)cm2 | C. | (3π+8)cm2 | D. | (3π+16)cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com