
【题目】已知{an}是公差为3的等差数列,数列{bn}满足b1=1,b2= ![]() ,anbn+1+bn+1=nbn .
,anbn+1+bn+1=nbn .
(1)求{an}的通项公式;
(2)求{bn}的前n项和.
【答案】
(1)
解:∵anbn+1+bn+1=nbn.
当n=1时,a1b2+b2=b1.
∵b1=1,b2= ![]() ,
,
∴a1=2,
又∵{an}是公差为3的等差数列,
∴an=3n﹣1
(2)
由(1)知:(3n﹣1)bn+1+bn+1=nbn.
即3bn+1=bn.
即数列{bn}是以1为首项,以 ![]() 为公比的等比数列
为公比的等比数列
∴{bn}的前n项和Sn= ![]() =
= ![]() (1﹣3﹣n)=
(1﹣3﹣n)= ![]() ﹣
﹣ ![]() .
.
【解析】(1)令n=1,可得a1=2,结合{an}是公差为3的等差数列,可得{an}的通项公式;(2)由(1)可得:数列{bn}是以1为首项,以 ![]() 为公比的等比数列,进而可得:{bn}的前n项和.;本题考查的知识点是数列的递推式,数列的通项公式,数列的前n项和公式,难度中档.
为公比的等比数列,进而可得:{bn}的前n项和.;本题考查的知识点是数列的递推式,数列的通项公式,数列的前n项和公式,难度中档.
【考点精析】认真审题,首先需要了解数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (a∈R).
(a∈R).
(Ⅰ)若f(1)=2,求函数y=f(x)-2x在[![]() ,2]上的值域;
,2]上的值域;
(Ⅱ)当a∈(0,![]() )时,试判断f(x)在(0,1]上的单调性,并用定义证明你的结论.
)时,试判断f(x)在(0,1]上的单调性,并用定义证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x﹣ ![]() sin2x+asinx在(﹣∞,+∞)单调递增,则a的取值范围是( )
sin2x+asinx在(﹣∞,+∞)单调递增,则a的取值范围是( )
A.[﹣1,1]
B.[﹣1, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣1,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(x+2)=f(x),且在[1,2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A. f![]()
![]()
![]() B. f
B. f![]()
![]()
![]()
C. f![]()
![]()
![]()
![]() D. f
D. f![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】借助计算机(器)作某些分段函数图象时,分段函数的表示有时可以利用函数![]() ,例如要表示分段函数g(x)=
,例如要表示分段函数g(x)=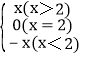 总可以将g(x)表示为g(x)=xh(x-2)+(-x)h(2-x).
总可以将g(x)表示为g(x)=xh(x-2)+(-x)h(2-x).
(1)设f(x)=(x2-2x+3)h(x-1)+(1-x2)h(1-x),请把函数f(x)写成分段函数的形式;
(2)已知G(x)=[(3a-1)x+4a]h(1-x)+logaxh(x-1)是R上的减函数,求a的取值范围;
(3)设F(x)=(x2+x-a+1)h(x-a)+(x2-x+a+1)h(a-x),求函数F(x)的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com