
分析 (1)求出原点到直线的距离,由圆的弦长公式可得2a=4,即a=2,由离心率可得c=1,求得b,进而得到椭圆方程;
(2)讨论两直线的斜率不存在和为0,求得弦长的比为1;再由直线y=k(x-1),代入抛物线的方程y2=4x,运用韦达定理和弦长公式,求得|MN|,再由直线y=-$\frac{1}{k}$(x-1),代入椭圆方程3x2+4y2-12=0,运用韦达定理和弦长公式,可得|AB|,化简整理,计算即可得到所求范围.
解答 解:(1)由圆心(0,0)到直线y=x+2的距离为d=$\frac{|2|}{\sqrt{2}}$=$\sqrt{2}$,
可得弦长为2$\sqrt{6-2}$=4,
由题意可得2a=4,即a=2,e=$\frac{c}{a}$=$\frac{1}{2}$,可得c=1,b=$\sqrt{4-1}$=$\sqrt{3}$,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)当互相垂直的直线一条斜率为0,另一条不存在,
可得|MN|=|AB|=4,即有$\frac{|AB|}{|MN|}$=1;
设互相垂直的直线中一条为y=k(x-1),代入抛物线的方程y2=4x,
可得k2x2-(2k2+4)x+k2=0,
x1+x2=2+$\frac{4}{{k}^{2}}$,x1x2=1,
即有弦长|MN|=$\sqrt{1+{k}^{2}}$•$\sqrt{(2+\frac{4}{{k}^{2}})^{2}-4}$=$\frac{4(1+{k}^{2})}{{k}^{2}}$,
将直线y=-$\frac{1}{k}$(x-1),代入椭圆方程3x2+4y2-12=0,
可得(4+3k2)x2-8x+4-12k2=0,
即有x3+x4=$\frac{8}{4+3{k}^{2}}$,x3x4=$\frac{4-12{k}^{2}}{4+3{k}^{2}}$,
弦长|AB|=$\sqrt{1+\frac{1}{{k}^{2}}}$•$\sqrt{\frac{64}{(4+3{k}^{2})^{2}}-\frac{16-48{k}^{2}}{4+3{k}^{2}}}$
=$\frac{12(1+{k}^{2})}{4+3{k}^{2}}$,
即有$\frac{|AB|}{|MN|}$=$\frac{3{k}^{2}}{4+3{k}^{2}}$=$\frac{3}{3+\frac{4}{{k}^{2}}}$∈(0,1).
综上可得,$\frac{|AB|}{|MN|}$的取值范围是(0,1).
点评 本题考查椭圆的方程的求法,注意运用离心率公式,考查弦长的求法,注意运用联立直线方程和曲线方程,运用韦达定理和弦长公式,考查化简整理的运算能力,属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①,②是真命题 | B. | ①是真命题,②是假命题 | ||
| C. | ①是假命题,②是真命题 | D. | ①,②都是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 等腰直角△ABC中,∠A=$\frac{π}{2}$,AC=1,BC在x轴上,有-个半径为1的圆P沿x轴向△ABC滚动,并沿△ABC的表面滚过,则圆心P的大致轨迹是(虚线为各段弧所在圆的半径)( )
等腰直角△ABC中,∠A=$\frac{π}{2}$,AC=1,BC在x轴上,有-个半径为1的圆P沿x轴向△ABC滚动,并沿△ABC的表面滚过,则圆心P的大致轨迹是(虚线为各段弧所在圆的半径)( )| A. | 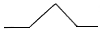 | B. |  | C. | 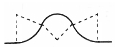 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 菜系 | 粤菜 | 川菜 | 鲁菜 | 东北菜 |
| 人数 | 20 | 15 | 15 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com