
已知函数f(x)= x3-
x3-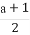 x2+x+b,其中a,b∈R.
x2+x+b,其中a,b∈R.
(1)若曲线y=f(x)在点P(2,f(2))处的切线方程为y=5x-4,求函数f(x)的解析式.
(2)当a>0时,讨论函数f(x)的单调性.
(1) f(x)=x3-2x2+x+4
(2) 当0<a<1时, >1,函数f(x)在区间(-∞,1)及(
>1,函数f(x)在区间(-∞,1)及( ,+∞)上为增函数,在区间(1,
,+∞)上为增函数,在区间(1, )上为减函数;
)上为减函数;
当a=1时, =1,函数f(x)在区间(-∞,+∞)上为增函数;
=1,函数f(x)在区间(-∞,+∞)上为增函数;
当a>1时, <1,函数f(x)在区间(-∞,
<1,函数f(x)在区间(-∞, )及(1,+∞)上为增函数,在区间(
)及(1,+∞)上为增函数,在区间( ,1)上为减函数.
,1)上为减函数.
【解析】(1)f'(x)=ax2-(a+1)x+1.
由导数的几何意义得f'(2)=5,于是a=3.
由切点P(2,f(2))在直线y=5x-4上可知2+b=6,解得b=4.
所以函数f(x)的解析式为f(x)=x3-2x2+x+4.
(2)f'(x)=ax2-(a+1)x+1=a(x- )(x-1).
)(x-1).
当0<a<1时, >1,函数f(x)在区间(-∞,1)及(
>1,函数f(x)在区间(-∞,1)及( ,+∞)上为增函数,在区间(1,
,+∞)上为增函数,在区间(1, )上为减函数;
)上为减函数;
当a=1时, =1,函数f(x)在区间(-∞,+∞)上为增函数;
=1,函数f(x)在区间(-∞,+∞)上为增函数;
当a>1时, <1,函数f(x)在区间(-∞,
<1,函数f(x)在区间(-∞, )及(1,+∞)上为增函数,在区间(
)及(1,+∞)上为增函数,在区间( ,1)上为减函数.
,1)上为减函数.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:选择题
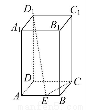
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=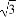 ,点E为AB上的动点,则D1E+CE的最小值为( )
,点E为AB上的动点,则D1E+CE的最小值为( )
(A)2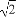 (B)
(B)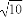
(C)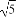 +1 (D)2+
+1 (D)2+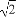
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十 第六章第六节练习卷(解析版) 题型:解答题
已知函数f(x)=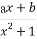 在点(-1,f(-1))处的切线方程为x+y+3=0.
在点(-1,f(-1))处的切线方程为x+y+3=0.
(1)求函数f(x)的解析式.
(2)设g(x)=lnx.求证:g(x)≥f(x)在[1,+∞)上恒成立.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十第二章第七节练习卷(解析版) 题型:填空题
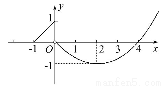
如图,定义在[-1,+∞)上的函数f(x)的图象由一条线段及抛物线的一部分组成,则f(x)的解析式为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十四第二章第十一节练习卷(解析版) 题型:选择题
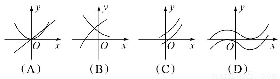
设f′(x)是函数f(x)的导函数,将y=f(x)和y=f′(x)的图象画在同一个直角坐标系中,不可能正确的是( )
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十六第二章第十三节练习卷(解析版) 题型:填空题
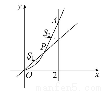
如图,设点P从原点沿曲线y=x2向点A(2,4)移动,记直线OP、曲线y=x2及直线x=2所围成的面积分别记为S1,S2,若S1=S2,则点P的坐标为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十八第三章第二节练习卷(解析版) 题型:填空题
已知α是第三象限角,且cos(85°+α)= ,则sin(α-95°)= .
,则sin(α-95°)= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:填空题
给出如下五个结论:
①存在α∈(0,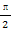 ),使sinα+cosα=
),使sinα+cosα= ;
;
②存在区间(a,b),使y=cosx为减函数而sinx<0;
③y=tanx在其定义域内为增函数;
④y=cos2x+sin(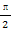 -x)既有最大值和最小值,又是偶函数;
-x)既有最大值和最小值,又是偶函数;
⑤y=sin|2x+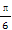 |的最小正周期为π.
|的最小正周期为π.
其中正确结论的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com