
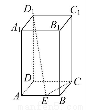
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=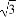 ,点E为AB上的动点,则D1E+CE的最小值为( )
,点E为AB上的动点,则D1E+CE的最小值为( )
(A)2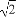 (B)
(B)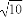
(C)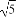 +1 (D)2+
+1 (D)2+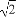
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十六第七章第五节练习卷(解析版) 题型:选择题
已知α,β,γ是三个不同的平面,命题“α∥β,且α⊥γ⇒β⊥γ”是真命题,如果把α,β,γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题有( )
(A)0个 (B)1个 (C)2个 (D)3个
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:选择题
如图,正方体ABCD-A'B'C'D'中,M,E是AB的三等分点,G,N是CD的三等分点,F,H分别是BC,MN的中点,则四棱锥A'-EFGH的侧视图为( )
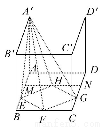
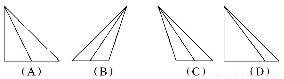
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:选择题
在正方体ABCD-A1B1C1D1中,二面角A1-BD-C1的余弦值为( )
(A)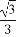 (B)
(B)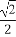 (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:解答题
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD.记CD=x,V(x)表示四棱锥F-ABCD的体积.
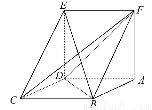
(1)求V(x)的表达式.
(2)求V(x)的最大值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:选择题
某几何体的三视图如图所示,且正视图、侧视图都是矩形,则该几何体的体积是( )
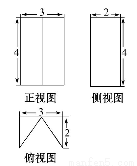
(A)16 (B)12 (C)8 (D)6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:填空题
已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三向量共面,则实数λ= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:填空题
已知f(n)=1+ +
+ +…+
+…+ (n∈N*),用数学归纳法证明f(2n)>
(n∈N*),用数学归纳法证明f(2n)> 时,f(2k+1)-f(2k)等于 .
时,f(2k+1)-f(2k)等于 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十四第二章第十一节练习卷(解析版) 题型:解答题
已知函数f(x)= x3-
x3-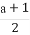 x2+x+b,其中a,b∈R.
x2+x+b,其中a,b∈R.
(1)若曲线y=f(x)在点P(2,f(2))处的切线方程为y=5x-4,求函数f(x)的解析式.
(2)当a>0时,讨论函数f(x)的单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com