(-
]

2

分析:A,由绝对值的几何意义可得f(x)=|x-1|+|x-m|的最小值为|m-1|,依题意,对m分m≤0与m>0讨论解决即可;
B,由题意可知,在△POD中,OD=1,OP=2,∠POD=120°,利用余弦定理即可求得PD的长;
C,将曲线(圆)的参数方程
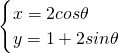
(θ为参数)化为标准方程,利用点到直线的距离公式可求得圆心(0,1)到直线3x-4y-1=0的距离为1,利用弦长之半,弦心距与圆的半径构成的直角三角形可求得截得的弦长.
解答:A,令f(x)=|x-1|+|x-m|,则f(x)
min=|m-1|,
∵|x-1|+|x-m|<2m的解集为∅,
∴当m≤0时,满足题意;
当m>0时,|m-1|≥2m>0,
解得0<m≤

;
综上所述,m≤

.
∴m的取值范围为(-∞,

];
B,依题意可知,OA⊥PA,在Rt△OAP中,OA=1,OP=2,
∴∠AOP=60°,
∴在△DOP中,∠DOP=120°,又OD=1,OP=2,
∴由余弦定理得PD
2=OD
2+OP
2-2OD•OPcos∠DOP
=1+4-2×1×2×(-

)
=7,
∴PD=

;
C,由圆的参数方程消掉参数可得其标准方程为:x
2+(y-1)
2=4,
∴该曲线是以C(0,1)为圆心,半径R=2的圆;设圆心C到直线3x-4y-1=0的距离为d,该直线与圆C相交的弦长为l,
则d=
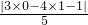
=1,
由弦心距,弦长之半,与该圆的半径组成直角三角形可知,

=

=

,
∴l=2

.
故答案为:(-∞,

];

;2

..
点评:本题A考查绝对值不等式,B考查与圆有关的比例线段,C考查圆的参数方程,考查分析转化与运算能力,属于基础题.

 A.若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为________.
A.若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为________.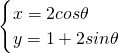 (θ为参数)所截得的弦长为________.
(θ为参数)所截得的弦长为________.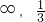 ]
]  2
2
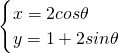 (θ为参数)化为标准方程,利用点到直线的距离公式可求得圆心(0,1)到直线3x-4y-1=0的距离为1,利用弦长之半,弦心距与圆的半径构成的直角三角形可求得截得的弦长.
(θ为参数)化为标准方程,利用点到直线的距离公式可求得圆心(0,1)到直线3x-4y-1=0的距离为1,利用弦长之半,弦心距与圆的半径构成的直角三角形可求得截得的弦长. ;
; .
. ];
]; )
) ;
;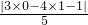 =1,
=1, =
= =
= ,
, .
. ];
]; ;2
;2 ..
..

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案 A.若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为
A.若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为 ,对任意的x∈R恒成立,则实数a的取值范围是______
,对任意的x∈R恒成立,则实数a的取值范围是______ (t为参数),圆C:ρ=2
(t为参数),圆C:ρ=2 cos(θ-
cos(θ- )(极轴与x轴的非负半轴重合,且单位长度相同),若直线l被圆C截得弦长为2,则a=______
)(极轴与x轴的非负半轴重合,且单位长度相同),若直线l被圆C截得弦长为2,则a=______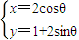 (θ为参数)所截得的弦长为 .
(θ为参数)所截得的弦长为 .