
【题目】已知圆O:x2+y2=r2(r>0),点P为圆O上任意一点(不在坐标轴上),过点P作倾斜角互补的两条直线分别交圆O于另一点A,B.
(1)当直线PA的斜率为2时,
①若点A的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),求点P的坐标;
),求点P的坐标;
②若点P的横坐标为2,且PA=2PB,求r的值;
(2)当点P在圆O上移动时,求证:直线OP与AB的斜率之积为定值.
【答案】
(1)解:①点A的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),代入可得r2=2
),代入可得r2=2
直线PA的方程为y+ ![]() =2(x+
=2(x+ ![]() ),即y=2x﹣1,
),即y=2x﹣1,
代入x2+y2=2,可得5x2﹣4x﹣1=0,∴点P的坐标为(1,1);
②因为直线PA与直线PB的倾斜角互补且直线PA的斜率为2,所以直线PB的斜率为﹣2.
设点P的坐标为(2,t),则直线PA的方程为:2x﹣y﹣4+t=0,直线PB的方程为:2x+y﹣t﹣4=0.
圆心(0,0)到直线PA,PB的距离分别为d1= ![]() ,d2=
,d2= ![]()
因为PA=2PB,所以由垂径定理得:4(r2﹣d12)=16(r2﹣d22)
所以4( ![]() )2﹣(
)2﹣( ![]() )2=3r2,
)2=3r2,
又因为点P(2,t)在圆O上,所以22+t2=r2(2),联立(1)(2)解得r= ![]() 或
或 ![]()
(2)解:由题意知:直线PA,PB的斜率均存在.
设点P的坐标为(x0,y0),直线OP的斜率为kOP= ![]()
直线PA的斜率为k,则直线PA的方程为:y﹣y0=k(x﹣x0),
联立直线PA与圆O方程x2+y2=r2,消去y得:
(1+k2)x2+2k(y0﹣kx0)x+(y0﹣kx0)2﹣r2=0,
因为点P在圆O上,即x02+y02=r2,
所以(y0﹣kx0)2﹣r2=(k2﹣1)x02﹣2kx0y0,
由韦达定理得:xA= ![]() ,故点A坐标为(
,故点A坐标为( ![]() ,
, ![]() ),
),
用“﹣k“代替“k“得:点B的坐标为( ![]() ,
, ![]() )
)
∴kAB= ![]() =
= ![]()
∴kABkOP=1.
综上,当点P在圆O上移动时,直线OP与AB的斜率之积为定值1
【解析】(1)①求出r2=2,直线PA的方程,代入x2+y2=2,可得5x2﹣4x﹣1=0,即可求点P的坐标;②若点P的横坐标为2,且PA=2PB,设点P的坐标为(2,t),由垂径定理得:4(r2﹣d12)=16(r2﹣d22),因为点P(2,t)在圆O上,所以22+t2=r2 , 即可求r的值;(2)当点P在圆O上移动时,求出A,B的坐标,即可证明直线OP与AB的斜率之积为定值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+2x+c的对称轴为x=1,g(x)=x+ ![]() (x>0).
(x>0).
(1)求函数g(x)的最小值及取得最小值时x的值;
(2)试确定c的取值范围,使g(x)﹣f(x)=0至少有一个实根;
(3)若F(x)=﹣f(x)+4x+c,存在实数t,对任意x∈[1,m],使F(x+t)≤3x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC. 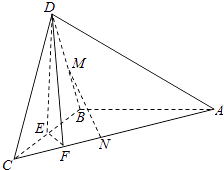
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN= ![]() CA,求证:MN∥平面DEF.
CA,求证:MN∥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(x+1)﹣f(x)=2x(x∈R),且f(0)=1.
(1)求f(x)的解析式;
(2)若关于x的方程f(x)=x+m有区间(﹣1,2)上有唯一实数根,求实数的取值范围(注:相等的实数根算一个).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆C1:(x﹣1)2+(y+3)2=1与圆C2:(x﹣a)2+(y﹣b)2=1外离,过直线l:x﹣y﹣1=0上任意一点P分别做圆C1 , C2的切线,切点分别为M,N,且均保持|PM|=|PN|,则a+b=( )
A.﹣2
B.﹣1
C.1
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com