
【题目】若圆C1:(x﹣1)2+(y+3)2=1与圆C2:(x﹣a)2+(y﹣b)2=1外离,过直线l:x﹣y﹣1=0上任意一点P分别做圆C1 , C2的切线,切点分别为M,N,且均保持|PM|=|PN|,则a+b=( )
A.﹣2
B.﹣1
C.1
D.2
【答案】A
【解析】解:设P(m,m﹣1),则
∵过直线l:x﹣y﹣1=0上任意一点P分别做圆C1,C2的切线,
切点分别为M,N,且均保持|PM|=|PN|,
∴|PC1|2﹣1=|PC2|2﹣1,
即(m﹣1)2+(m﹣1+3)2﹣1=(m﹣a)2+(m﹣1﹣b)2﹣1,
即(4+2a+2b)m+5﹣a2﹣(1+b)2=0,
∴4+2a+2b=0且5﹣a2﹣(1+b)2=0,
∴ ![]() 或
或 ![]() ,
,
∵圆C1:(x﹣1)2+(y+3)2=1与圆C2:(x﹣a)2+(y﹣b)2=1外离,
∴ ![]() >2,
>2,
∴a=﹣3,b=1,
∴a+b=﹣2,
故选A.
【考点精析】掌握直线与圆的三种位置关系是解答本题的根本,需要知道直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.


科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=r2(r>0),点P为圆O上任意一点(不在坐标轴上),过点P作倾斜角互补的两条直线分别交圆O于另一点A,B.
(1)当直线PA的斜率为2时,
①若点A的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),求点P的坐标;
),求点P的坐标;
②若点P的横坐标为2,且PA=2PB,求r的值;
(2)当点P在圆O上移动时,求证:直线OP与AB的斜率之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() +
+ ![]() )x3(a>0,a≠1).
)x3(a>0,a≠1).
(1)讨论函数f(x)的奇偶性;
(2)求a的取值范围,使f(x)+f(2x)>0在其定义域上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知△ABC的顶点A(5,1),B(1,5).
(1)若A为直角△ABC的直角顶点,且顶点C在y轴上,求BC边所在直线方程;
(2)若等腰△ABC的底边为BC,且C为直线l:y=2x+3上一点,求点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间D上的函数f(x),如果满足:对任意x∈D,都存在常数M≥0,有|f(x)|≤M,则称f(x)是区间D上有界函数,其中M称为f(x)上的一个上界,已知函数g(x)=log ![]() 为奇函数.
为奇函数.
(1)求函数g(x)在区间[ ![]() ,
, ![]() ]上的所有上界构成的集合;
]上的所有上界构成的集合;
(2)若g(1﹣m)+g(1﹣m2)<0,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥A﹣BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4 ![]() ,CD=4
,CD=4 ![]() ,∠ACB=45°,E,F分别为MN的中点.
,∠ACB=45°,E,F分别为MN的中点. 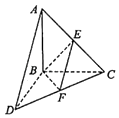
(1)求证:EF∥平面ABD;
(2)求二面角E﹣BF﹣C的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com