
【题目】已知函数f(x)=tan(ωx﹣![]() )(ω>0)的最小正周期为2π.
)(ω>0)的最小正周期为2π.
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)求不等式f(x)>﹣1的解集.
【答案】解:(Ⅰ)由函数f(x)=tan(ωx﹣![]() )(ω>0)的最小正周期为2π,
)(ω>0)的最小正周期为2π,
可得![]() =2π,∴ω=
=2π,∴ω=![]() ,f(x)=tan(
,f(x)=tan(![]() x﹣
x﹣![]() ).
).
令kπ﹣![]() <
<![]() x﹣
x﹣![]() <kπ+
<kπ+![]() ,k∈Z,求得2kπ﹣
,k∈Z,求得2kπ﹣![]() <x<2kπ+
<x<2kπ+![]() ,
,
故函数的定义域为(2kπ﹣![]() ,2kπ+
,2kπ+![]() ),k∈Z.
),k∈Z.
(Ⅱ)∵不等式f(x)>﹣1,即tan(![]() x﹣
x﹣![]() )>﹣1,即 kπ﹣
)>﹣1,即 kπ﹣![]() <
<![]() x﹣
x﹣![]() <kπ+
<kπ+![]() ,
,
求得 2kπ﹣![]() <x<2kπ+
<x<2kπ+![]() ,故不等式的解集为{x|kπ﹣
,故不等式的解集为{x|kπ﹣![]() <x<kπ+
<x<kπ+![]() ,k∈Z}.
,k∈Z}.
【解析】(Ⅰ)根据正切函数的周期性求得ω的值,可得函数的解析式,从而求得它的定义域.
(Ⅱ)由条件利用正切函数的图象,解三角不等式,求得x的范围.
【考点精析】根据题目的已知条件,利用正切函数的周期性的相关知识可以得到问题的答案,需要掌握正切函数的周期为![]() .
.


科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83. 
(1)求x和y的值;
(2)计算甲班7位学生成绩的方差s2;
(3)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形ABCD中,E,G分别是BC,DC上的点且 ![]() =3
=3 ![]() ,
, ![]() =3
=3 ![]() ,DE与BG交于点O.
,DE与BG交于点O. 
(1)求| ![]() |:|
|:| ![]() |;
|;
(2)若平行四边形ABCD的面积为21,求△BOC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象向右平移三个单位长度得到图象C,再将图象C上的所有点的横坐标变为原来的![]() 倍(纵坐标不变)得到图象C1 , 则C1的函数解析式为
倍(纵坐标不变)得到图象C1 , 则C1的函数解析式为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
A.9.4,0.484
B.9.4,0.016
C.9.5,0.04
D.9.5,0.016
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥 ![]() 的底面为正方形,
的底面为正方形, ![]() ⊥底面
⊥底面 ![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )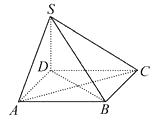
A.![]()
B.![]() ∥平面
∥平面 ![]()
C.![]() 与
与 ![]() 所成的角等于
所成的角等于 ![]() 与
与 ![]() 所成的角
所成的角
D.![]() 与平面
与平面 ![]() 所成的角等于
所成的角等于 ![]() 与平面
与平面 ![]() 所成的角
所成的角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=r2(r>0),点P为圆O上任意一点(不在坐标轴上),过点P作倾斜角互补的两条直线分别交圆O于另一点A,B.
(1)当直线PA的斜率为2时,
①若点A的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),求点P的坐标;
),求点P的坐标;
②若点P的横坐标为2,且PA=2PB,求r的值;
(2)当点P在圆O上移动时,求证:直线OP与AB的斜率之积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com