Question

【题目】在平行四边形ABCD中，E，G分别是BC，DC上的点且 =3 ， =3 ，DE与BG交于点O．
（1）求| |：| |；
（2）若平行四边形ABCD的面积为21，求△BOC的面积．

Answer 1

【答案】
（1）解：由于D、O、E共线，故有 =λ =λ（ ﹣ ）．

∵B、O、G共线，∴ =m +（1﹣m） =m（﹣ ）+（1﹣m）（ ）

=﹣ m +（1﹣m）（ ﹣ ）= + ，

∴ = + ，

∴λ（ ﹣ ）= + ，

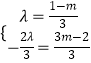∴ ，求得λ= ，

可得| |：| |=

（2）解：由（1）可得△BOC 与△BDC的高之比 = ，∴△BOC 与△BDC的面积之比为 = ，

∴S△BOC= S△BDC= =

【解析】（1）由D、O、E共线，故有 =λ =λ（ ﹣ ）．再由 B、O、G共线，求得 = + ，再利用平面向量基本定理求得λ 的值，即可得到结论．（2）由（1）可得 = ，可得 = ，再根据S△BOC= S△BDC ， 计算求得结果．
【考点精析】根据题目的已知条件，利用正弦定理的定义的相关知识可以得到问题的答案，需要掌握正弦定理:．