
【题目】已知函数g(x)=Asin(ωx+φ)(其中A>0,|φ|< ![]() ,ω>0)的图象如图所示,函数f(x)=g(x)+
,ω>0)的图象如图所示,函数f(x)=g(x)+ ![]() cos2x﹣
cos2x﹣ ![]() sin2x
sin2x 
(1)如果 ![]() ,且g(x1)=g(x2),求g(x1+x2)的值;
,且g(x1)=g(x2),求g(x1+x2)的值;
(2)当﹣ ![]() ≤x≤
≤x≤ ![]() 时,求函数f(x)的最大值、最小值及相应的x值;
时,求函数f(x)的最大值、最小值及相应的x值;
(3)已知方程f(x)﹣k=0在 ![]() 上只有一解,则k的取值集合.
上只有一解,则k的取值集合.
【答案】
(1)解:由图象得,A=1,
![]() T=
T= ![]() ,则
,则 ![]() ,所以ω=2,
,所以ω=2,
把点 ![]() 代入得,sin(2×
代入得,sin(2× ![]() +φ)=0,则2×
+φ)=0,则2× ![]() +φ=kπ,
+φ=kπ,
解得 ![]() (k∈Z),由﹣π<<0得,
(k∈Z),由﹣π<<0得, ![]() ,
,
所以 ![]() ,
,
因为 ![]() ,且g(x1)=g(x2),
,且g(x1)=g(x2),
所以由图得, ![]() ,
,
则 ![]()
(2)解:由(1)得,f(x)=g(x)+ ![]() cos2x﹣
cos2x﹣ ![]() sin2x
sin2x
= ![]() =
= ![]() ,
,
因为 ![]() ,所以
,所以 ![]() ,
,
当 ![]() 时,即
时,即 ![]() 时,ymax=2,
时,ymax=2,
当 ![]() 时,即
时,即 ![]() 时,
时, ![]()
(3)解:由(2)得,f(x)= ![]() ,
,
因为x∈ ![]() ,所以
,所以 ![]() ∈
∈ ![]() ,
,
则 ![]() ,
,
即 ![]() ,
,
因为方程f(x)﹣k=0在 ![]() 上只有一解,
上只有一解,
则k的取值集合是(﹣ ![]() ,
, ![]() ]∪{﹣2}
]∪{﹣2}
【解析】(1)由图象求出A、T、ω和φ,求出g(x)的解析式,由图象和条件求出x1+x2的值,代入解析式由特殊角的正弦函数求g(x1+x2)的值;(2)由(1)和两角和、差的正弦公式化简f(x),由x的范围、正弦函数的性质,求出答案;(3)由x∈ ![]() 求出
求出 ![]() 的范围,由正弦函数的性质求出
的范围,由正弦函数的性质求出 ![]() 的范围,由条件和方程的根转化求出k的取值集合.
的范围,由条件和方程的根转化求出k的取值集合.
【考点精析】通过灵活运用三角函数的最值,掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,E是PC的中点,求证: (Ⅰ)PA∥平面EDB
(Ⅱ)AD⊥PC.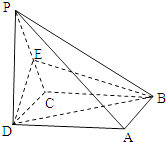
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆与双曲线有相同的焦点F1(﹣c,0),F2(c,0),椭圆的一个短轴端点为B,直线F1B与双曲线的一条渐近线平行,若椭圆与双曲线的离心率分别为e1 , e2 , 则3e12+e22的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形ABCD中,E,G分别是BC,DC上的点且 ![]() =3
=3 ![]() ,
, ![]() =3
=3 ![]() ,DE与BG交于点O.
,DE与BG交于点O. 
(1)求| ![]() |:|
|:| ![]() |;
|;
(2)若平行四边形ABCD的面积为21,求△BOC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象向右平移三个单位长度得到图象C,再将图象C上的所有点的横坐标变为原来的![]() 倍(纵坐标不变)得到图象C1 , 则C1的函数解析式为
倍(纵坐标不变)得到图象C1 , 则C1的函数解析式为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥 ![]() 的底面为正方形,
的底面为正方形, ![]() ⊥底面
⊥底面 ![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )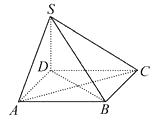
A.![]()
B.![]() ∥平面
∥平面 ![]()
C.![]() 与
与 ![]() 所成的角等于
所成的角等于 ![]() 与
与 ![]() 所成的角
所成的角
D.![]() 与平面
与平面 ![]() 所成的角等于
所成的角等于 ![]() 与平面
与平面 ![]() 所成的角
所成的角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 为偶函数,且函数的y=f(x)图象相邻的两条对称轴间的距离为
为偶函数,且函数的y=f(x)图象相邻的两条对称轴间的距离为 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)将y=f(x)的图象向右平移 ![]() 个单位后,再将所得的图象上个点的横坐标伸长为原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求y=g(x)的单调区间,并求其在
个单位后,再将所得的图象上个点的横坐标伸长为原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求y=g(x)的单调区间,并求其在 ![]() 上的最值.
上的最值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com