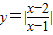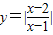练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数（ ）
    A．在（1，+∞）上单调递增
    B．在（1，2）上单调递增
    C．在（1，+∞）上单调递减
    D．在（1，2）上单调递减
    【答案】分析：当1＜x＜2时，将函数函数化成 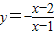的解析式变形后，根据函数图象的平移变换法则我们可得函数的图象是由反比例函数 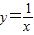的图象向右平移一个单位再向下平移一个单位得到的，结合反比例函数 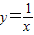的性质及及函数图象平移法则，易得到结论．
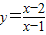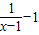    解答：解：函数 =的图象是由函数 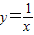的图象向右平移一个单位再向下平移一个单位得到的，
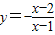    故函数函数 在区间（1，2）上都单调递减；
    分析四个答案中，易得只有D符合要求；
    故选D．
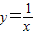    点评：本题考查的知识点是带绝对值的函数、函数的图象，其中根据原函数解析式判断出函数的图象是由函数 的图象向右平移一个单位再向下平移一个单位得到的，从而将一个非基本函数转化为研究一个基本初等函数的图象和性质是解答本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知向量
    a
    =(x，1)    ，
    b
    =(x，tx+2)    ．若函数f(x)=
    a
    •
    b
    在区间[-1，1]上不是单调函数，则实数t的取值范围是
    （-2，2）
    （-2，2）
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量a=(x2，x+1)，b=(1-x，t).若函数f(x)=a·b在区间(-1，1)上是增函数，求t的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量a=(x2,x+1),b=(1-x,t).若函数f(x)=a·b在区间(-1,1)上是增函数,求t的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：2004-2005学年上海市十校高三联考数学试卷（文科）（解析版） 题型：选择题

    函数（ ）
    A．在（-1，1）上单调递增
    B．在（-1，0）上单调递增，在（0，1）上单调递减
    C．在（-1，1）上单调递减
    D．在（-1，0）上单调递减，在（0，1）上单调递增

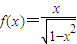    查看答案和解析>>

    同步练习册答案